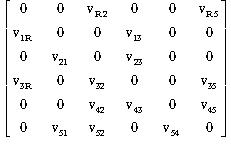VODOPRIVREDNI SISTEMI

PISMENI ISPITNI ROKOVI
GRA\EVINSKI FAKULTET
UNIVERZITETA U BEOGRADU

PISMENI ISPIT IZ VODOPRIVRENIH SISTEMA
05.07.2000.
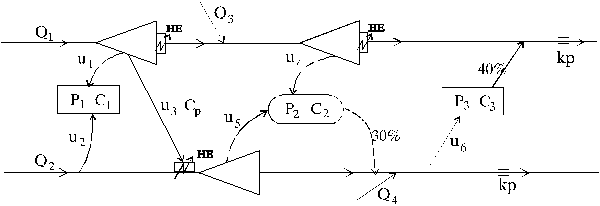
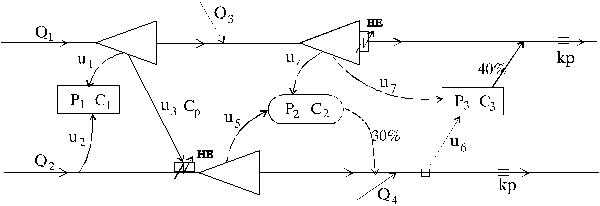
ZADATAK 1. Na skici je dat planirani vodoprivredni sistem. Investicioni tro{kovi akumulacija su funkcija korisne zapremine, a dobiti su linearna funkcija od primljene koli~ine vode.

Oznake na slici: P - potreba za vodom, C1 i C2 - jedini~na dobit od isporu~ene vode, Ce - cena (dobit) energije, qmin - zahtevani protok (garantovani ekolo{ki protok).

Napisati jedna~ine matemati~kog modela, relacije ograni~enja i ekonomsku kriterijumsku funkciju za optimizaciju sistema.

ZADATAK 2. Razmatra se sistem prikazan na skici. Potrebe korisnika za vodom su 5 m3/s, a neophodno mu je isporu~iti 80% od zahtevanih koli~ina. Voda se korisniku mo`e isporu~iti iz dva izvora A i B. Izda{nost izvora A je 5 m3/s, a izvora B je 2.5 m3/s. Za zadovoljavanje potrebe korisnika od 1 m3/s potrebno je isporu~iti iz izvora A 1.6 m3/s, a iz izvora B 1.4 m3/s (zbog gubitaka u sistemu).

a) Napisati matemati~ki model za optimizaciju linearnim programiranjem, dati grafi~ku interpretaciju re{enja i odrediti optimalne vrednosti koli~ina vode koje dobija korisnik iz izvora A i B. Jedini~ni tro{kovi kod izvora A su CA=2 10n din/m3/s, a kod izvora B su CB=3 10n din/m3/s.

b) Zadatak pod a) pro{iruje se uvo|enjem i jedini~ne dobiti po m3/s dobijene vode kod korisnika, iz izvora A CKA=3.5 10n din/m3/s i iz izvora B CKB=3.8 10n din/m3/s. Re{iti ovaj pro{ireni zadatak na na~in kao pod a).

ZADATAK 3. Kriterijumska funkcija za optimalno upravljanje akumulacijom ima slede}i oblik:

gde je: c - koeficijent za vrednovanje {tete, um - isporu~ena koli~ina vode u m-tom mesecu. Korisna zapremina je W=6 106 m3, a po~etna zapremina vode u akumulaciji Vo=3 106m3. Vrednosti dotoka Q (106 m3) , potrebe za vodom i koeficijenti {tete c za vremenski horizont od 5 meseci dati su tabelarno.

m

1

2

3

4

5

Qm (106 m3)

6

4

5

4

3

Pm (106 m3)

3

4

6

5

4

cm

1

2

1

2

1

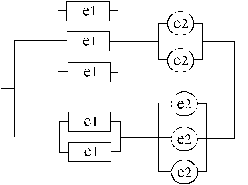
Napisati rekurentnu relaciju dinami~kog programiranja i ograni~enja na koordinate stanja i upravljanja, a zatim primenom dinami~kog programiranja odrediti optimalnu trajektoriju stanja akumulacije i optimalno upravljanje. Komentarisati re{enje.

ZADATAK 4. Sistem je prikazan na skici. Pouzdanost jednog elementa e1 iznosi 0,7, a elementa e2 0,6.

a) Odrediti pouzdanost celog sistema.

b) Koliko najmanje elemenata e2 treba dodati (samo u jedan od podsistema) pa da pouzdanost celog sistema na bude manja od 0,99? Komentarisati re{enje.

c) Kolika je pouzdanost sistema ako je za pravilan rad neophodno da rade najmanje dva elementa e2 i najmanje jedan element e1?

Predmetni nastavnik:
Prof. dr Branislav \or|evi}
GRA\EVINSKI FAKULTET
UNIVERZITETA U BEOGRADU

PISMENI ISPIT IZ VODOPRIVRENIH SISTEMA
31. 01. 2001.
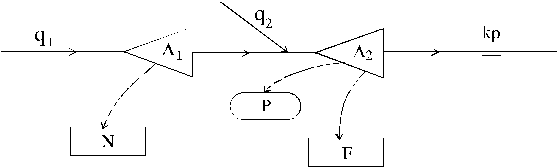
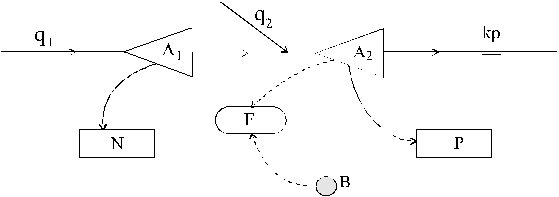
ZADATAK 1. Planira se izgradnja vodoprivrednog sistema prikazanog na skici.

Akumulacija A1, korisne zapremine 6 106 m3, slu`i za navodnjavanje povr{ine od 2000 ha, sa vrednostima hidromodula datim u tabeli. Iz akumulacije A2 snabdeva se vodom naselje od 120000 stanovnika, sa specifi~nom potro{njom 360 l/standan, sa koeficijentima neravnomernosti potro{nje datim u tabeli. Nizvodno od akumulacije A2 zahteva se da proticaj ne bude manji od 0.2 m3/s. Vrednosti dotoka date su u tabeli.

m

1

2

3

4

5

6

7

8

9

10

11

12

q1 (m3/s)

0.18

0.12

0.22

0.95

0.74

1.3

2.1

0.6

0.27

0.16

0.1

0.07

q2 (m3/s)

1.0

1.4

0.9

1.8

1.7

0.4

0.6

0.6

1.1

0.7

0.6

1.2

km

0.8

0.8

0.9

1.0

1.05

1.1

1.2

1.2

1.1

1.0

0.95

0.9

nm (m3/ha mes)

0

0

0

0

500

2100

2650

1800

700

0

0

0

Pretpostaviti da na po~etku vremenskog horizonta analize u akumulaciji A1 ima vode ~ija je zapremina jednaka 60% od korisne zapremine.

a) Odrediti korisnu zapreminu akumulacije A2.

b) Odrediti za koliko se mora pove}ati korisna zapremina akumulacije A2, u odnosu na izra~unatu pod a), ako se u sistem doda korisnik F (sistem za navodnjavanje povr{ine 1000 ha, ~ija su vrednost hidromodula iste kao kod korisnika N).

ZADATAK 2. Iz jednog izvori{ta snabdevaju se vodom dva korisnika A i B (videti skicu). Izda{nost izvora je 5.5 m3/s. Potrebe za vodom korisnika A su 3 m3/s, pri ~emu korisnik mora dobiti 75% od potrebnih koli~ina. Iz lokalnih izvori{ta korisnik A obezbe|uje 0.5 m3/s. Potrebe za vodom korisnika B su 2.3 m3/s, a korisnik mora dobiti 80% od tih koli~ina. Korisnik B iz lokalnih izvori{ta obezbe|uje 0.3 m3/s. Gubici vode od izvora do korisnika A su 20%, a do korisnika B su 30%.

  • a) Napisati matemati~ki model za optimizaciju linearnim programiranjem, dati grafi~ku interpretaciju re{enja i odrediti optimalne vrednosti koli~ina vode koje se isporu~uju iz izvori{ta. Jedini~ni tro{kovi po m3/s isporu~ene vode iz izvora prema korisniku A su CA=2 10n din/m3/s, a prema korisniku B su CB=1.5 10n din/m3/s.

    b) Zadatak pod a) pro{iruje se uvo|enjem jedini~ne dobiti po m3/s dobijene vode kod korisnika A CKA=3.5 10n din/m3/s i kod korisnika B CKB=4.2 10n din/m3/s. Re{iti ovaj pro{ireni zadatak na na~in kao pod a).

    c) Koja ograni~enja su aktivna, za oba dela zadatka (a i b), i za{to?

    •

    ZADATAK 3. Kriterijumska funkcija za optimalno upravljanje akumulacijom ima slede}i oblik:

    gde je: c - koeficijent za vrednovanje {tete, um - isporu~ena koli~ina vode u m-tom mesecu. Korisna zapremina je W=4 106 m3, a po~etna zapremina vode u akumulaciji Vo=2 106 m3. Vrednosti dotoka Q (106 m3), potrebe za vodom i koeficijenti dobiti c za vremenski horizont od 5 meseci dati su tabelarno.

    m

    1

    2

    3

    4

    5

    Qm (106 m3)

    4

    4

    5

    3

    1

    Pm (106 m3)

    3

    4

    4

    5

    5

    cm

    1

    2

    1

    2

    3

    Napisati rekurentnu relaciju dinami~kog programiranja i ograni~enja na koordinate stanja i upravljanja, a zatim primenom dinami~kog programiranja odrediti optimalnu trajektoriju stanja akumulacije i optimalno upravljanje.

    ZADATAK 4. [ematski prikazati sistem koji je definisan slede}om matricom veza:

    Predmetni nastavnik
    Prof. dr Branislav \or|evi}
    GRA\EVINSKI FAKULTET
    UNIVERZITETA U BEOGRADU

    PISMENI ISPIT IZ VODOPRIVRENIH SISTEMA
    03. 03. 2001.
    ZADATAK 1. Na skici je dat planirani vodoprivredni sistem. Investicioni tro{kovi akumulacija su funkcija korisne zapremine, a dobiti su linearna funkcija od primljene koli~ine vode.

    Oznake na slici: P - potreba za vodom, C1 i C2 - jedini~na dobit od isporu~ene vode, Ce - cena energije, Cp - cena prevo|enja vode, qmin - zahtevani protok (garantovani ekolo{ki protok).

    Napisati jedna~ine matemati~kog modela, relacije ograni~enja i ekonomsku kriterijumsku funkciju za optimizaciju sistema.

    ZADATAK 2. Dat je vodoprivredni sistem prikazan na skici.

    Iz akumulacije A1 (korisne zapremine 7 106 m3) snabdeva se vodom naselje N od 90000 stanovnika, sa specifi~nom potro{njom 360 l/stan dan, sa koeficijentima neravnomernosti potro{nje datim u tabeli. Akumulacija A2 slu`i za navodnjavanje povr{ine P od 1800 ha, sa vrednostima hidromodula datim u tabeli. Nizvodno od akumulacije A2 zahteva se da proticaj ne bude manji od 0,5 m3/s. Vrednosti dotoka date su u tabeli.

    Pretpostaviti da na po~etku vremenskog horizonta analize u akumulacijama ima vode ~ija je zapremina jednaka 50% od korisne zapremine.

    U ovaj sistem uvodi se korisnik F - sistem za navodnjavanje povr{ine 2200 ha, koji ima iste zahteve za vodom kao korisnik P.

    Odrediti:

    1. Za koliko se mora pove}ati korisna zapremina akumulacije A2 ako se korisniku F sva potrebna voda isporu~uje iz te akumulacije.

    2. Kolike su u{tede (u odnosu na slu~aj 1) ako se deo potreba korisnika F podmiruje iz lokalnog izvori{ta B, ~iji je kapacitet 900 l/s. Ukupni tro{kovi pove}anja korisne zapremine akumulacije A2 za 1 106 m3 su 4.5 10x din, a ukupni tro{kovi kaptiranja izvori{ta B su 5 10x din.

    ZADATAK 3. Sa jednog izvori{ta snabdeva se vodom naselje od 120000 stanovnika, pri ~emu su tro{kovi isporuke vode 1 NJ/(l/s) (NJ - nov~ana jedinica). Specifi~na potro{nja naselja je 360 l/stan dan, a neophodno mu je isporu~iti 75% od zahtevanih koli~ina. Cena vode je 1.5 NJ/(l/s). Kanalizacioni sistem je separacionog tipa, a njime se u vidu fekalne kanalizacije odvodi 65% od isporu~ene vode. Jedan deo ovih voda odlazi na postrojenje za pre~i{}avanje, a drugi deo se ispu{ta direktno u reku. Kapacitet postrojenja za pre~i{}avanje otpadne vode je 150 l/s, radi sa stepenom pre~i{}avanja od 80%, a cena pre~i{}avanja je 0.5 NJ/(l/s). Naknada za ispu{tanje otpadne vode u reku je 0.7 NJ/(l/s).

    Napisati matemati~ki model za optimizaciju koli~ine vode koja se isporu~uje naselju i optadnih voda koje se iz naselja ispu{taju u reku.

    ZADATAK 4. Kriterijumska funkcija za optimalno upravljanje akumulacijom ima slede}i oblik:

    gde je: c - koeficijent za vrednovanje {tete, um - isporu~ena koli~ina vode u m-tom mesecu. Korisna zapremina je W = 5 106 m3, a po~etna zapremina vode u akumulaciji Vo = 2 106 m3. Vrednosti dotoka Q (106 m3) , potrebe za vodom i koeficijenti {tete c za vremenski horizont od 5 meseci dati su tabelarno.

    m

    1

    2

    3

    4

    5

    Qm (106 m3)

    5

    4

    5

    3

    1

    Pm (106 m3)

    3

    4

    4

    5

    5

    cm

    1

    2

    1

    2

    3

    Napisati rekurentnu relaciju dinami~kog programiranja i ograni~enja na koordinate stanja i upravljanja, a zatim primenom dinami~kog programiranja odrediti optimalnu trajektoriju stanja akumulacije i optimalno upravljanje. Pretpostaviti da na kraju razmatranog perioda akumulacija ne sme biti prazna.

    Predmetni nastavnik:
    Prof. dr Branislav \or|evi}