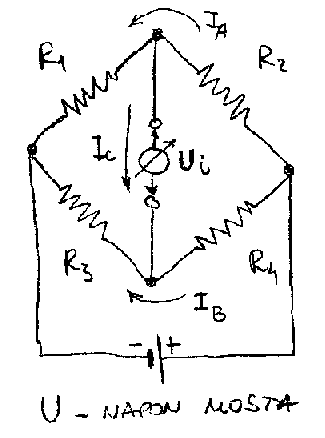Merenja u hidrotehnici

Dusan Prodanovi\'c

`"

Contents

5  (10) Opste o merenju u hidrotehnici
    5.1  Direktno merenje velicina
    5.2  Posredno merenje velicina - merni pretvaraci
        5.2.1  Podela mernih pretvaraca za posredno merenje
        5.2.2  Osnovne karakteristike mernih pretvaraca
            5.2.2.1  Ponovljivost
            5.2.2.2  Stabilnost
            5.2.2.3  Rezolucija
            5.2.2.4  Linearnost
            5.2.2.5  Merni opseg
            5.2.2.6  Uslovi ugradnje i koris\'cenja pretvaraca
            5.2.2.7  Idealan merni pretvarac

List of Figures

    5.1  Mereni pritisak se konvertuje u pomeranje vrha elasticne cevi Dx
    5.2  Kalibracija - postupak uporedjenja posredne merne velicine sa poznatom velicinom
    5.3  Mehanicki merni pretvaraci - pomeranje, rotacija, ...
    5.4  Elektricni merni pretvaraci - induktivni, kapacitivni, ultrazvucni, ...
    5.5  Kod elektricnih mernih pretvaraca se cesto koristi Vitstonov most
    5.6  Vitstonov most za merenje pomeranja pomo\'cu mernih traka - razlicite merne konfiguracije
    5.7  Vitstonov most sa povratnom spregom, cesto se koristi za Hot-film anemometriju
    5.8  Ponovljivost mernog pretvaraca
    5.9  Petlja u krivoj protoka [28]
    5.10  Stabilnost mernog pretvaraca kroz vreme i pri promeni spoljnih uslova
    5.11  Kalibracija kapacitivnog pretvaraca dubine vode pri razlicitim temperaturama ambijenta [19]
    5.12  Kalibracija kapacitivnog pretvaraca [40]
    5.13  Rezolucija analognog i digitalnog mernog pretvaraca
    5.14  Rezolucija digitalnog AD konvertera
    5.15  Linearnost mernog pretvaraca
    5.16  Linearizacija nelinearnog davaca [40]
    5.17  Frekventni opseg mernog pretvaraca

Chapter 5
Opste o merenjima hidrotehnickih velicina



U hidrotehninci se najces\'ce mere slede\'ce velicine:
  1. Iz grupe osnovnih velicina, kako su definisane medjunarodnim sistemom mera (SI):
    • Duzina - duzina cevovoda, precnik cevi, dubina vode, povrsina rezervoara zapremina ....
    • Masa, odnosno tezina
    • Vreme
    • Temperatura
  2. Izvedene velicine
    • Pritisak
    • Brzina
    • Protok
    • Parametri kvaliteta - koncentracija materija, mutno\'ca, elektro provodnost ...
    • ...


Najtacniji nacin merenja je direktno uporedjivanje sa etalonom iste vrste i to je takozvano direktno merenje ili apsolutno merenje.


Merenje nize tacnosti je kada se meri neka druga fizicka velicina, koja je u nekoj relaciji sa zeljenom mernom velicinom. U merenju se koriste merni pretvaraci. Takvo merenje se naziva posredno merenje i uvek zahteva medjukorak, kalibraciju mernih pretvaraca.





5.1  Direktno merenje velicina



Zbog visoke tacnosti direktnog merenja, i njene vaznosti radi metroloske uredjenosti u zemlji, kao i zbog potrebe da se ispostuju medjunarodni standardi, drzava se stara o etalonima pomo\'cu zakona i propisa - uveden je sistem etalona kojime se odrzava merna sledivost:
  1. primarni etaloni - cuvaju se na jednom mestu i samo sluze da se pomo\'cu njih kontrolisu sekundarni etaloni,
  2. sekundarni etaloni - da se umnozi primarni, treba da ga imaju kontrole mera,
  3. radni etaloni - za rad po terenu (redovno se proveravaju pomo\'cu sekundarnih etalona).


Apsolutno merenje je ako se neka velicina direktno poredi sa radnim etalonom. Na primer: merenje mase na terazijama - direktno se uporedjuje merena masa sa etaloniziranim tegovima.


Apsolutno merenje je i ako se izvedena velicina dobije kao odnos osnovnih velicina. Na primer: pritisak p je sila po jedinici povrsine A:
p= F
A
 = m   g
A
Sila se dobija merenjem mase tega m, direktnim uporedjenjem sa etalonom mase, a povrsina A se dobija merenjem neke duzine, opet direktnim uporedjenjem sa etalonom.


Apsolutno merenje, kao merenje sa najnizom mernom neizvesnos\'cu, se po pravilu koristi u metroloskim laboratorijama, dok se u realnim uslovima koristi samo u situacijama gde je to mogu\'ce.





5.2  Posredno merenje velicina - merni pretvaraci



Svaka izvedena merna velicina se moze svesti na kombinaciju osnovnih velicina, odakle sledi da je mogu\'ce uvek primeniti apsolutno merenje. Na zalost, to nije uvek izvodljivo, pa se ces\'ce koriste merni pretvaraci koji posredno mere fizicku velicinu preko neke druge fizicke velicine.


Primer: Pritisak, koji moze apsolutno da se izmeri, uglavnom se meri mehanickim manometrom - meri se pomeranje vrha savijene cevi Dx = f ( p ) , slika 5.1.


Figure 5.1: Mereni pritisak se konvertuje u pomeranje vrha elasticne cevi Dx
../SlikePng/Mpuvod01.png


Funkcija preslikavanja f(p) mora da se odredi za svaki pojedini komad pretvaraca postupkom koji se zove kalibracija1: uporedjenjem pomeranja Dx i poznate velicine p odredjene tacnijom metodom, obicno apsolutnim merenjem.


Primer kalibracije pretvaraca pritiska je dat na slici 5.2, gde se koristi osnovni princip da je pritisak u nestisljivom fluidu na istoj koti konstantan: pomo\'cu tega poznate mase i klipa poznate povrsine, na manometar se dovodi pritsak p=[(mg)/(A)]. Na kalibracionom dijagramu se mogu nanositi parovi tacaka m,Dx, gde je Dx pomeranje cevi u manometru (kao sto je dato na slici 5.2, ili, mnogo upotrebljivije, parovi tacaka p,a, gde je a ugao otklona kazaljke na manometru.
Figure 5.2: Kalibracija - postupak uporedjenja posredne merne velicine sa poznatom velicinom
../SlikePng/Mpuvod02.png


Na slede\'coj slici je dat primer komercijalnog etalon klipnih manometara
Kalibrator firme DRUCK  (slika preuzeta sa:www.druck.com)


Sam naziv merni pretvaraci dolazi od toga sto oni pretvaraju mehanicku energiju u drugi vid mehanicke ili u elektricnu energiju.





5.2.1  Podela mernih pretvaraca za posredno merenje



Osnovna podela mernih pretvaraca je prema energiji u koju se transformise merna velicina:
  1. Mehanicki - vodomer, manometar, rotametar, ... (stare proverene konstrukcije, masovni, jeftini, nize tacnosti, ... slika 5.3)


    Figure 5.3: Mehanicki merni pretvaraci - pomeranje, rotacija, ...
    ../SlikePng/Mpuvod03.png
  2. Elektricni - induktivni manometri, kapacitivni nivometar, UZV merac protoka, laserski anemometri, ... (merenje neelektricnih velicina elektricnim putem, slika 5.4)


    Figure 5.4: Elektricni merni pretvaraci - induktivni, kapacitivni, ultrazvucni, ...
    ../SlikePng/Mpuvod04.png
Kod ve\'cine savremenih mernih pretvaraca, koristi se visestruka konverzija energije. Na primer, pretvaraci pritiska najces\'ce rade na slede\'ci nacin:


Elektricni pretvaraci se sve ces\'ce sre\'cu, najces\'ce imaju ve\'cu tacnost, povoljni su za daljinski prenos i automatsko belezenje podataka. Kod ve\'cine elektricnih pretvaraca se koristi Vitstonov most, na slici 5.5 (Wheatsone).


Figure 5.5: Kod elektricnih mernih pretvaraca se cesto koristi Vitstonov most
../SlikePng/Mpuvod05.png
Da bi Vitstonov most bio u ravnotezi Ui = 0 potrebno je ostvariti:

U1 = U3

U2 = U4
Znaci, ako je:
R1IA = R3IB

R2IA = R4IB
tada je izlazni napon Ui = 0 . Odatle sledi:
Ui = U1 - U3 = R1 ×IA - R3 ×IB

IA = U
R1 + R2

IB = U
R3 + R4
zato sto je Ui=0, odnosno, struja kroz instrument Ic = 0 .

Ui = R1 × U
R1 + R2
 - R3 × U
R3 + R4

Ui = U × R1 ( R3 + R4 ) - R3 ( R1 + R2 )
( R1 + R2 ) ( R3 + R4 )

Ui = U × R1 ×R4 - R3 ×R2
( R1 + R2 ) ( R3 + R4 )
(5.1)
Dobijena je zavisnost izlaznog napona Ui od vrednosti otpornika u Vitstonovom mostu. Da bi se most doveo u ravnotezu, izbalansirao, odnosno da bi se postiglo Ui = 0 u neporeme\'cenom stanju, potrebno je ostvariti:
R1 ×R4 = R3 ×R2 Þ R1 ×R4
R3 ×R2


Kod mernih traka menja se otpornost sa istezanjem - mogu\'ce su slede\'ce konfiguracije primene Vitstonovog mosta (slika 5.6):
Figure 5.6: Vitstonov most za merenje pomeranja pomo\'cu mernih traka - razlicite merne konfiguracije
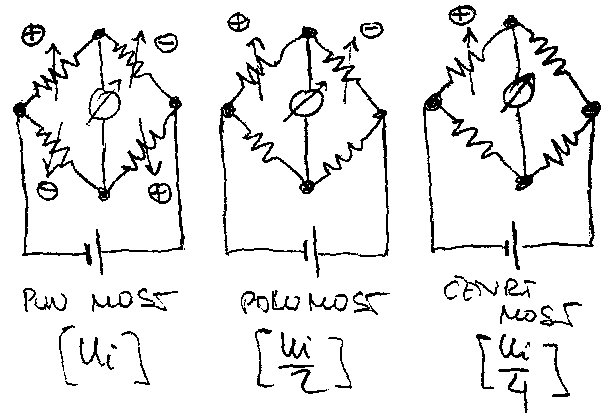
../SlikePng/Mpuvod06.png


Koja je prednost koris\'cenja Vitstonovog mosta? Merne trake (kao i ve\'cina drugih elektricnih pretvaraca) su osetljive ne samo na istezanje (korisna osetljivost) ve\'c i na temperaturu, vlaznost, elektricne smetnje i druge uticaje. Ako su sve cetri grane mosta izlozene istim smetnjama, za izbalansiran most se iz izraza 5.1 moze videti da \'ce izlazni napon Ui ostati nula! Odnosno, izlazni napon \'ce biti proporcionalan samo izduzenju merne trake, a ne i ostalim smetnjama.


Uobicajeni problemi sa kojima se bore elektricni merni pretvaraci su:


Merni most se koristi i kod induktivnih i kapacitivnih davaca. Tada je otpornost R zamenjena kompleksnom otpornos\'cu R, C, L a pobudni napon U je naizmenicni, sinusni, konstantne frekvencije (obicno 1 ili 2 KHz).


Merni most se koristi cesto kod aktivnih pretvaraca sa povratnom spregom, slika 5.7.


Figure 5.7: Vitstonov most sa povratnom spregom, cesto se koristi za Hot-film anemometriju
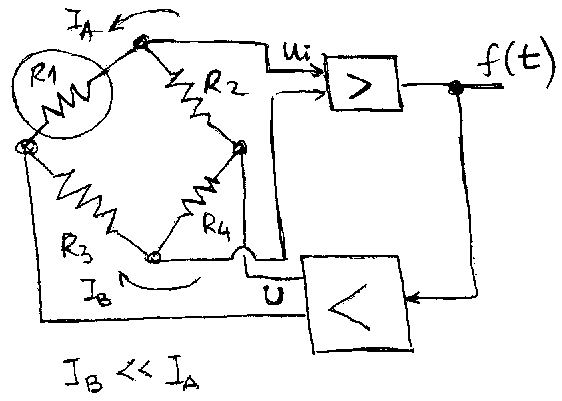../SlikePng/Mpuvod07.png
Princip rada mosta sa povratnom spregom, u primeru hot-film anemometrije, je slede\'ci: otpornici R2, R3 i R4 (sa slike 5.7) su konstantni, a R1 je izlozen spoljnom hladjenju usled prolaska vode. Napon napajanja mosta U nije konstantan, ve\'c je promenljiv, tako da se struja IA menja. Elektronika tako menja napon napajanja mosta, da odrzava otpornost R1 na istoj temperaturi (princip rada Hot film anemometra). Sto je ve\'ca brzina vode, ve\'ce je hladjenje otpornika R1 pa je i ve\'ci napon napajanja mosta U.
(OVO JOS MALO DETALJNIJE OBJASNITI)


Pored podele mernih pretvaraca na mehanicke i elektricne, u literaturi se mogu na\'ci i slede\'ce podele [4]:
Prema koris\'cenju energije
  1. Aktivne - oni pretvaraci koji koriste energiju velicine koju mere i pretvaraju je u drugu energiju: elektromagnetski, piezoelektricni, termoelektricni, fotoelektricni, ...
  2. Pasivne - pretvaraci koji zahtevaju dodatni izvor energije i ne remete velicine koje mere: otporni pretvaraci, induktivni, kapacitivni, ...
Prema kontaktu sa merenim objektom
  1. Kontaktni - moraju biti u kontaktu sa mernom velicinom (ve\'cina konvencionalnih pretvaraca radi na tom principu), pri cemu je cesto uticaj pretvaraca na merenu velicinu nezanemarljiv,
  2. Bezkontaktni - daljinski se meri velicina: infracrveni senzori (IC), ultrazvucni (UZV), laserski, radarski, .... Pogodnost je sto ne remete merenu velicinu.
Prema tacnosti
Klasa tacnosti se odredjuje kao verovatna relativna neizvesnost u odnosu na maksimalnu mernu velicinu, u procentima:
e = s[`(j)]
|jNPMAX|
gde je s[`(j)] = [( sj)/(ÖN)] standardna greska srednje vrednosti ili neodredjenost najverovatnije procene, kako daju proizvodjaci, ili u odnosu na trenutnu vrednost kako je korisnicima vaznije: e = [(s[`(j)] )/(|jNP|)] ×100 % .
Prema klasi tacnosti, merni pretvaraci se mogu podeliti na slede\'ce kategorije:
  1. Visoka klasa tacnosti e » 0.1 %
  2. Za naplatna merila je klasa tacnosti e » 0.5 %
  3. Industrijska klasa, odnosno za nadzor procesa je obicno e » 1 %
  4. Vodomeri, kalorimetri i drugi masovni uredjaji e » 2 do 5 %
Prema brzini rada
Podela se vrsi prema brzini rada, odnosno prema frekvenciji fN (izraz  na strani ) do koje je pretvarac u stanju da prenese nepromenljive fluktuacije merene velicine:
  1. Spori pretvaraci - fN < 1 [Hz]
  2. Brzi pretvaraci - uglavnom elektricni, za pra\'cenje fluktuacija merene velicine. Kod brzih pretvaraca bitna je transfer funkcija za sâm pretvarac.





5.2.2  Osnovne karakteristike mernih pretvaraca



Tacnost, odnosno klasa tacnosti mernog pretvaraca je jedan od osnovnih parametara. Taj parametar najvise interesuje korisnika i pokazuje kolika je merna neizvesnost u koris\'cenju pretvaraca.


Tacnost mernog pretvaraca se utvrdjuje kalibracionim merenjem, formiranjem kalibracione krive. Medjutim, tacnost, ili klasa tacnosti ne zavisi samo od kalibracije pretvaraca, ve\'c i od niza drugih parametara, koji \'ce se detaljnije obraditi u nastavku.





5.2.2.1  Ponovljivost



Ponovljivost znaci da se za istu ulaznu velicinu merenog signala dobija isti izlaz iz pretvaraca, bez obzira na to da li je ulazna velicina u fazi opadanja ili porasta.


Figure 5.8: Ponovljivost mernog pretvaraca
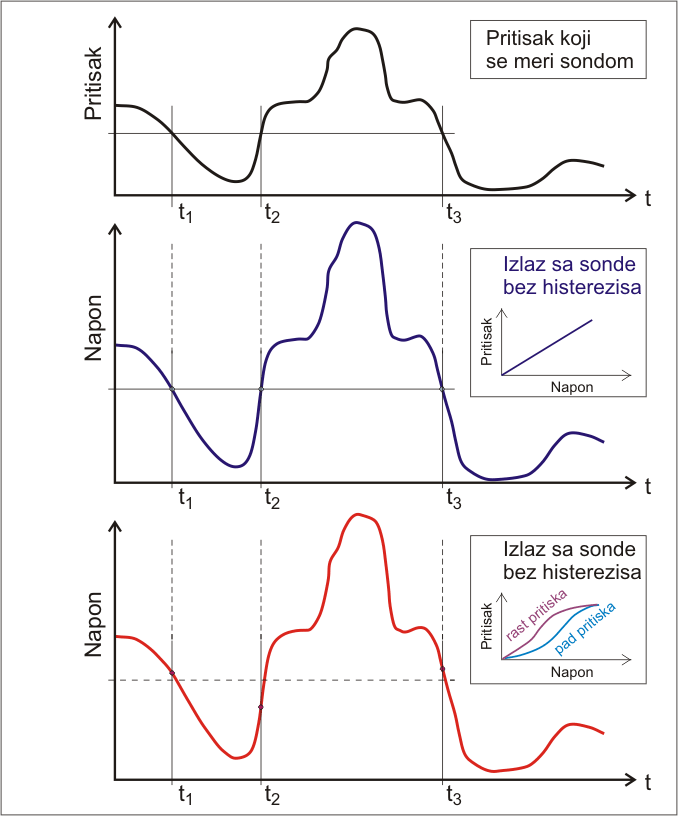
../SlikePng/Mpuvod08.png


Histerezis mernog pretvaraca direktno odredjuje njegovu ponovljivost. Histerezis moze biti rezultat rada samog mernog pretvaraca ili usled posrednog merenja neke velicine pri cemu sam proces u sebi nosi histerezis (merenje protoka preko nivoa vode u rekama).


Figure 5.9: Petlja u krivoj protoka [28]
../SlikePng/Q-H-KrivaSaPetljom-Jasha.png


Dobra ponovljivost ne znaci automatski i dobru tacnost. Pretvarac moze biti ponovljiv ali netacan (usled lose kalibracije, klizanja, losih radnih uslova ili neke druge sistematske greske).


Pretvarac sa losom ponovljivo\'cu se, medjutim, nikakvim merama ne moze dovesti do visoke klase tacnosti.


U poglavlju o greskama je takodje dat primer ponovljivosti i tacnosti.
Ponovljivost versus tacnost-1 Internet LINK
Ponovljivost versus tacnost-1 Internet LINK


Pogledati uporedjenje ponovljivosti i tacnosti Slika preuzeta iz knjige [14] - strana 19





5.2.2.2  Stabilnost



Stabilnost mernog pretvaraca je, posle ponovljivosti, drugi po vaznosti parametar koji utice na klasu tacnosti. Stabilnost se prati:
Figure 5.10: Stabilnost mernog pretvaraca kroz vreme i pri promeni spoljnih uslova
../SlikePng/Mpuvod09.png


Pogledati primer kako se u katalozima merne opreme obicno daje podatak o dugortajnoj stabilnosti.


Na slede\'cem dijagramu je prikazan rezultat kalibracije pretvaraca za merenje nivoa, koji je temperaturno osetljiv. Raspon mogu\'cih merenih vrednosti dubine, za ocitanu dubinu na pisacu SC od 10 mm je od 19 cm za letnju kalibraciju do 28 cm za sezonu ranog prole\'ca i kasne jeseni!. Ako se uzme srednja vrednost (sto nije dobro!) tada je 23.5 cm tacna merena vrednost, a odstupanja su ±20%, za pretvarac koji je imao deklarisanu tacnost od 1%!


Figure 5.11: Kalibracija kapacitivnog pretvaraca dubine vode pri razlicitim temperaturama ambijenta [19]
../SlikePng/ThermalDriftOfLevelProbe.png


Naravno, nisu sve kapacitivne sonde tako lose. Na slede\'coj slici se daje rezultat ispitivanja temperaturne stabilnosti dosta kvalitetnije sonde. Uociti i histerezis koji se javlja.


Figure 5.12: Kalibracija kapacitivnog pretvaraca [40]
../SlikePng/UticajTemperatureNaKapacitivnuSondu-Vojt.png


Podsetimo se i dijagrama sonde za merenje pritiska kada je izlozimo temperaturnoj promeri (prikazano u prethodnom poglavlju) - prvi deo slike:


Figure 4.18: Temperaturna stabilnost merenja nivoa u SOLINST logeru
../SlikePng/Solinst-TemperaturnaStabilnost.png





5.2.2.3  Rezolucija



Rezolucija je mo\'c razlucivanja izmedju dve najmanje promene merene velicine.


Kod analognih pretvaraca, kontinualno promenljiva ulazna velicina se preslikava u kontinualno promenljiv izlaz, tako da je, teorijski, rezolucija beskonacno velika.
U praksi, rezolucija analognih pretvaraca je jednaka sumu koji je uvek prisutan.


Figure 5.13: Rezolucija analognog i digitalnog mernog pretvaraca
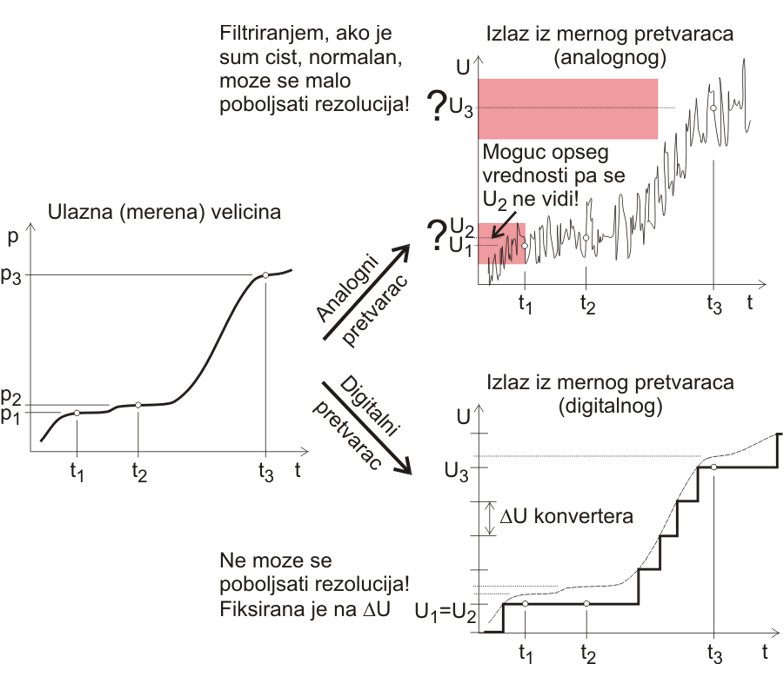../SlikePng/Rezolucija-AnalogniIDigitalniSignal.png
Kod digitalnih pretvaraca, kontinualno promenljiva ulazna velicina se diskretizuje u konacan broj izlaznih naponskih intervala DU, pa je rezolucija jednaka koraku DU.


Primer: Signal generator generise sinusoidu 250 Hz izlaznog napona (relativno) 1 V. Pojacanje na ulazu digitalnog osciloskopa je 3.24 puta Sinusoida 250 Hz. Ako se smanji izlazni napon generatora 10 puta, a pokazivanje na osciloskopu "razvuce" 7.53/3.24=2.32 puta, na osciloskopu \'ce se pojaviti "stepenast" signal, vidi se greska usled konacne rezolucije digitalnog signala Losa sinusoida 250 Hz.


Figure 5.14: Rezolucija digitalnog AD konvertera
../SlikePng/RezolucijaAD-Primer.jpg


(U materijalu se ne prica mnogo o AD konverziji. Rezolucija je direktno vezana za to. Lep tekst je u knjizi The Scientists and Engineer's Guide to Digital Signal Processing - Steven Smith - o postupku A-D konverzije prvi deo poglavlja 3 (link ne radi na Internet prezentaciji). Samo slika iz knjige koja to ilustruje: DSP-Slika-3-1.png (link ne radi na Internet prezentaciji).)





5.2.2.4  Linearnost



Treba razlikovati linearnost samog mernog pretvaraca (na primer, sonde za merenje nivoa vode) od lineranosti ukupnog sistema u kome posredno merimo neku velicinu (na primer nivo vode) da bi odredili neku drugu (na primer, protok na prelivu preko izmerenog nivoa vode).
Linearni sistemi su zgodni za koris\'cenje, jer u celom opsegu imaju istu rezoluciju. Nelinearni su komplikovaniji za obradu, moze da se desi da je rezolucija slabija u opsegu koji nam treba. Primer: ostroivicni Thompsonov preliv, za velike protoke manja rezolucija - isto Dh ne daje isto DQ za malo Q i za veliko Q!


Figure 5.15: Linearnost mernog pretvaraca
../SlikePng/Mpuvod10.png


NelinearnostKapacitivneSonde-Vojt.png
Nelinearnost samih senzora se najces\'ce tretira kao greska merne opreme. Ako je ta nelinearnost ponovljiva, moze se pazljivom kalibracijom i linearizacijom smanjiti ukupna greska. Na slede\'coj slici je dat primer kalibracije kapacitivne sonde i greske koje su rezultat fabricke kalibracije (linearne) i nelinearne (polinomom tre\'ceg stepena).


Figure 5.16: Linearizacija nelinearnog davaca [40]
../SlikePng/NelinearnostKapacitivneSonde-Vojt.png


Proizvodjaci opreme su duzni da daju podatak o linearnosti mernog davaca. Pogledati primer kako se u katalozima merne opreme obicno daje podatak o linearnosti, kombinovanoj sa histerezisom i ponovljivos\'cu. Kod ovoh uredjaja je linearnost strujnog izlaza problematicna!





5.2.2.5  Merni opseg



Merni opseg pretvaraca se posmatra u vremenskom i frekventnom domenu:


Figure 5.17: Frekventni opseg mernog pretvaraca
../SlikePng/Mpuvod11.png





5.2.2.6  Uslovi ugradnje i koris\'cenja pretvaraca



Nacin ugradnje i uslovi pod kojima se pretvarac koristi ne spadaju u osnovne parametre mernog pretvaraca, ali mogu znacajno da umanje klasu njegove tacnosti.


Za svaki tip pretvaraca, proizvodjac treba eksplicitno da navede te uslove, a ozbiljniji proizvodjaci cak daju i procenu degradacije merne tacnosti ukoliko se neki od uslova ne ispune.





5.2.2.7  Idealan merni pretvarac



Kada bi postojao idealan merni pretvarac on bi morao da ispunjava slede\'ce uslove:
  1. Klase tacnosti koja je dovoljna za razmatrani problem,
  2. Ponovljiv, da radi bez histerezisa
  3. Stabilan kroz vreme, da izlaz ne "klizi" sa starenjem,
  4. Termostabilan, da izlaz ne zavisi od promene temperature ambijenta,
  5. Neutralan, da ne utice na merenu velicinu
  6. Linearan, da je izlaz oblika Ui=k X + U0, gde se k i U0 odredjuju kalibracijom,
  7. Visoke sopstvene frekvencije, tako da je ispunjeno fN >> fMER
  8. Izlazni signal dovoljnog nivoa za dalju obradu, memorisanje ili prenos,
  9. Jeftin i robustan, i na kraju,
  10. Pravilno ugradjen.





Bibliography

[1]
Ackers, P., W.R. White, J.A. Perkins i A.J.M. Harrison. (1978). Weirs and Flumes for Flow Measurement. John Wiley & Sons. Chichester.
[2]
Baker, R. C (2000). Flow measurement handbook: industrial designs, operating principles, performance, and applications. Cambridge University Press.
[3]
Benedict, R.P. (1969). Fundamentals of Temperature, Pressure and Flow Measurements. John Wiley & Sons. New York.
[4]
Boros, A. (1985). Electrical Measurements in Engineering. Akadémiai kiadó. Budapest.
[5]
Bos, M.G., J.A. Replogle i A.J. Clemmens. (1984). Flow Measuring Flumes for Open Channel Systems. John Wiley & Sons. New York.
[6]
Camnasio, E., E. Orsi. (2008). Experimenting with a new calibration method for current meters. 7th international conference on hydraulic efficiency measurements (IGHEM), Milano (http://www.ighem.org/IGHEM2008/home.html).
[7]
Chow, V.T. (1959). Open-channel Hydraulics. McGraw-Hill. Tokyo.
[8]
Drenthen, J.G. (1987). Accoustic Discharge Measuring Devices. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[9]
Durst, F. (1987). Discharge Measuring Methods in Pipes. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[10]
Eckelmann, H. (1987). Hot-film and Hot-wire Anemometers. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[11]
Endress, U. (1987). Vortex Shedding Flow Meters. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[12]
Fingerston, L.M. (1987). An Introduction to Laser Doppler Anemometry. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[13]
Gaji\'c, A., Lj. Krsmanovi\'c. (1994). Matematicka analiza i postupci eksperimentalnih istrazivanja. Masinski fakultet, Univerzitet u Beogradu.
[14]
Hayward, A.T.J. (1979). Flowmeters: A Basic Guide and Source-book for Users. Macmillan publishers Ltd, London.
[15]
Hajdin, G. (1977). Mehanika fluida - Knjiga prva: Osnove. Gradjevinski fakultet Beograd.
[16]
Henderson, F.M. (1966). Open Channel Flow. The Macmillan Company. New York.
[17]
Jovanovi\'c, S., O. Bonacci i M. Andjeli\'c. (1977). Hidrometrija. Gradjevinski fakultet Beograd.
[18]
Mass, H.G., A. Gruen i D. Papantoniou. (1992). Particle Tracking Velocimetry in Three Dimensional Turbulent Flows - Part I: Photogrammetric Determination of Particle Coordinates. Flow Visualization and Flow Structures. Short course by IAHR program of continuing education. Editor: A. Müler.
[19]
Maksimovi\'c, C., J. Despotovi\'c, P. Trisi\'c, M. Simi\'c. (1986). Accuracy and reliability of rainfall and runoff measurements - Examples. Urban Drainage Modelling - Supplements. Editori: C. Maksimovi\'c and M. Radojkovi\'c. Dubrovnik.
[20]
Maksimovi\'c, C. (1993). Merenja u hidrotehnici. Gradjevinski fakultet Beograd.
[21]
Malik, N.A., T. Dracos, D. Papantoniou i H.G. Maas. (1992). Particle Tracking Velocimetry in Three Dimensional Turbulent Flows - Part II: Particle Tracking and Lagrangian Trajectories. Flow Visualization and Flow Structures. Short course by IAHR program of continuing education. Editor: A. Müler.
[22]
Merzkirch, W. (1987). Methods of Flow Visualization. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[23]
Merzkirch, W. (1992). Methods of Flow Visualization. Flow Visualization and Flow Structures. Short course by IAHR program of continuing education. Editor: A. Müler.
[24]
Mettlen, D. (1987). Mass Flow Measurement. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[25]
Miller, R.W. (1983). Flow Measurement Engineering Handbook. McGraw-Hill. New York.
[26]
Müller, A. i H.G. Maas. (1992). Methods of Flow Visualization. Flow Visualization and Flow Structures. Short course by IAHR program of continuing education. Editor: A. Müler.
[27]
Nakayama, Y. i R.F. Boucher. (1999). Introduction to Fluid Mechanics. Arnold. London.
[28]
Plavsi\'c, J. (2007). Skripta za predmet Inzenjerska hidrologija. Gradjevinski fakultet Univerziteta u Beogradu.
[29]
Prodanovi\'c, D. (1985). Diplomski rad... Diplomski rad. Gradjevinski fakultet Univerziteta u Beogradu.
[30]
Prodanovi\'c, D., A. Spoljari\'c, M. Iveti\'c i C. Maksimovi\'c. (1985). Dynamic characteristics of a pressure measuring system. Symposium on Measuring Techniques in Hydraulic Research. Delft.
[31]
Prodanovi\'c, D. (1992). Eksperimentalno izucavanje uticaja dva tipa regulacionih zatvaraca na fluidnu struju. Magistarski rad. Gradjevinski fakultet Univerziteta u Beogradu.
[32]
Prodanovi\'c, D. (2007). Mehanika fluida za studente Gradevinskog fakulteta. Gradjevinski fakultet Univerziteta u Beogradu.
[33]
Patel, V.C. (1987). An Introduction to Measurement of Velocity. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[34]
Radojkovi\'c, M., D. Obradovi\'c i C. Maksimovi\'c. (1989). Primena racunara u komunalnoj hidrotehnici. Naucna knjiga. Beograd.
[35]
Rouse, H. i S. Ince. (1957). History of Hydraulics. Iowa Institute of Hydraulic Reserach. Iowa City.
[36]
Stankovi\'c, D. (1997). Fizicko tehnicka merenja: Senzori. Univerzitet u Beogradu.
[37]
Staubli, T. (1987). Propeller-type Current Meters. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.
[38]
Taylor, J.R. (1982). An Introduction to Error Analysis. Oxford University Press.
[39]
Utami, T. i T. Ueno. (1987). Experimental Study on the Coherent Structure of Turbulent Open-channel Flow Using Visualization and Picture Processing. Journal of Fluid Mechanics. Knjiga 174, strane 399-440.
[40]
Vojt, P. (2006). Pove\'canje tacnosti merenja nivoa vode kapacitivnom sondom sa primenom na hidraulickoj analizi vodostana sa prigusivacem. Diplomski rad. Gradjevinski fakultet Univerziteta u Beogradu.
[41]
Westerweel, J. (1992). Particle Image Velocimetry. Flow Visualization and Flow Structures. Short course by IAHR program of continuing education. Editor: A. Müler.
[42]
White, W.R. (1987). Discharge Measuring Methods in Open Channels. Discharge and Velocity Measurement. Short course by IAHR Section on Hydraulics Instrumentation. Editor: A. Müler.

Footnotes:

1 Cesto je upotrebi rec bazdarenje, ali se ona iskljucivo odnosi na definisanje podele na nekoj skali pri cemu se uglavnom radi o zapremini ili eventualno masi - dakle osnovnim velicinama u direktnom merenju.

File translated from TEX by TTH, version 3.85.
On 20 Oct 2010, 08:24.