
|
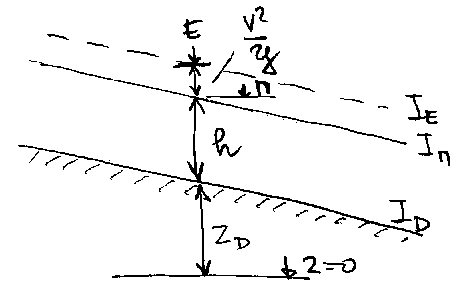
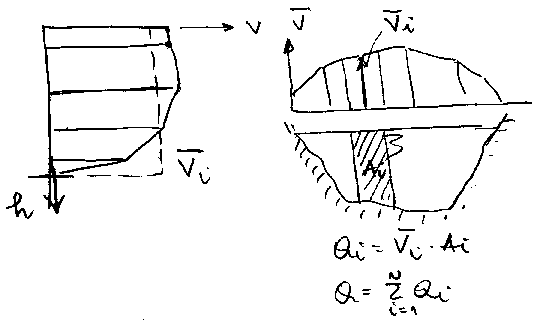
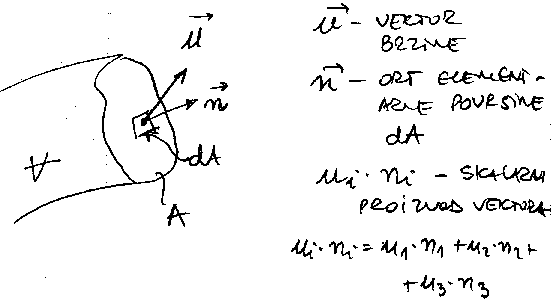 Na slici 9.2 je prikazan vektor brizne
[(u)\vec] koji u opstem slucaju nije upravan na elementarnu
povrsinu dA. Ako je [(n)\vec] ort elementarne povrsine dA,
tada je ui ·ni skalarni
proizvod dva vektora:
Na slici 9.2 je prikazan vektor brizne
[(u)\vec] koji u opstem slucaju nije upravan na elementarnu
povrsinu dA. Ako je [(n)\vec] ort elementarne povrsine dA,
tada je ui ·ni skalarni
proizvod dva vektora:
|
|
|


|
|

|

|

|
Literatura: Cedo Maksimovic, MERENJA U HIDROTEHNICI, 1993., deo II
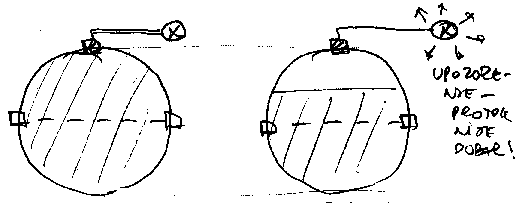
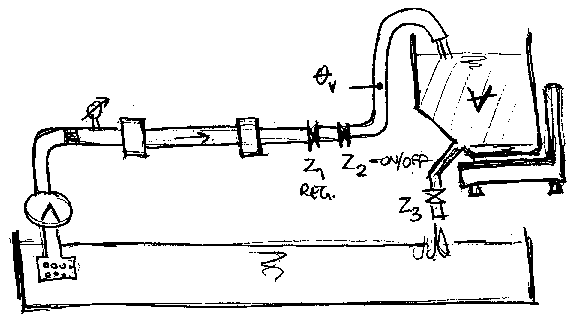
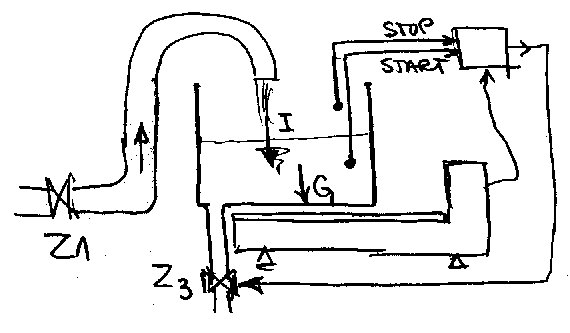
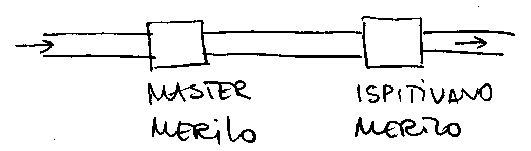
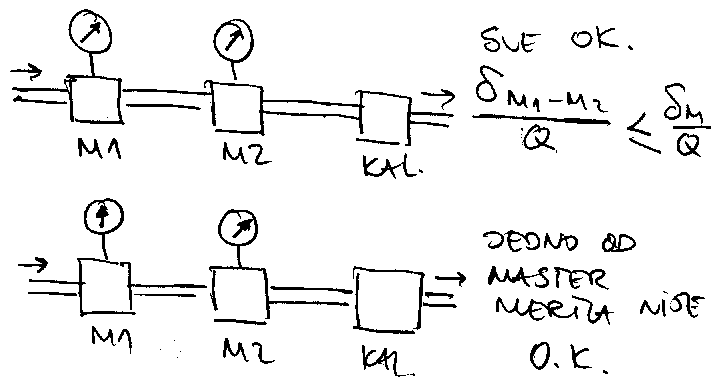
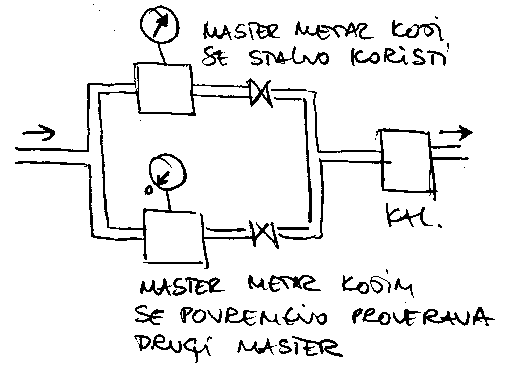
 Merenje u kolektorima (posebno kisnim) trazi
vise paznje, jer kolektor moze povremeno do\'ci pod pritisak, pa
pretpostavljene relacije o vezi merne velicine i protoka vise ne vaze.
Mogu\'ca su tri resenja:
Merenje u kolektorima (posebno kisnim) trazi
vise paznje, jer kolektor moze povremeno do\'ci pod pritisak, pa
pretpostavljene relacije o vezi merne velicine i protoka vise ne vaze.
Mogu\'ca su tri resenja:

|
|
|

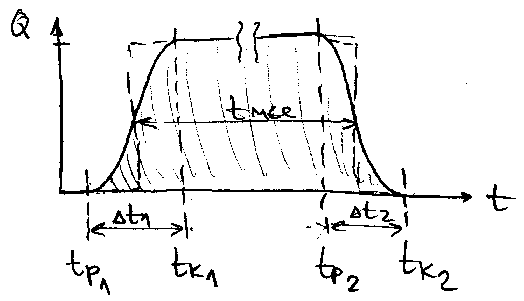
 Potrebno je dovoljno merenja za razlicite protoke Q, uvodi se
pojam modula protoka, ...
Potrebno je dovoljno merenja za razlicite protoke Q, uvodi se
pojam modula protoka, ... 
|
|
(9.2) |
|
(9.3) |
|
(9.4) |
|
|
|
(9.5) |
|
|
|
|
|
|
|
|
|
|


|
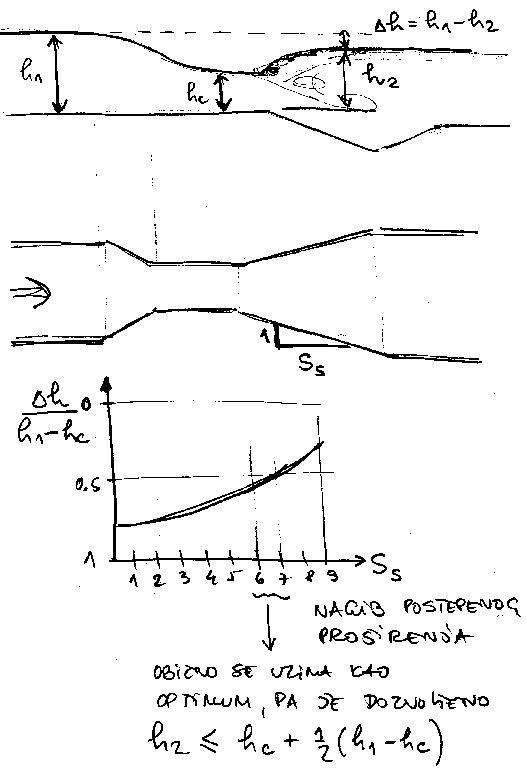
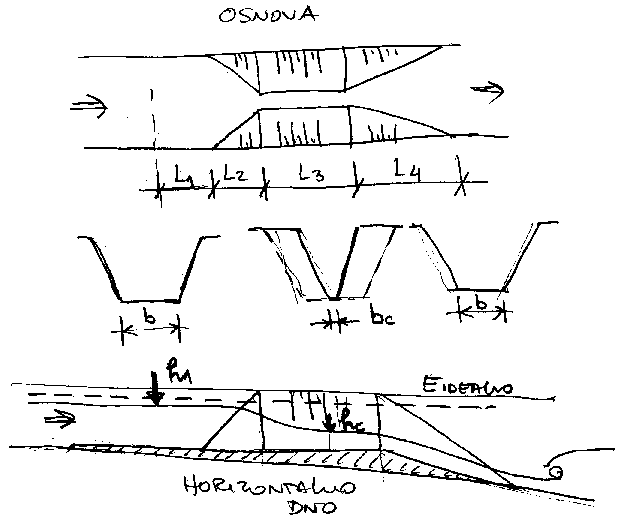
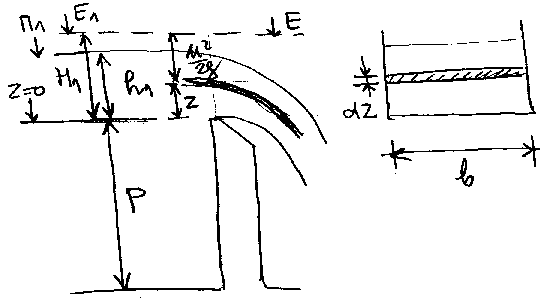
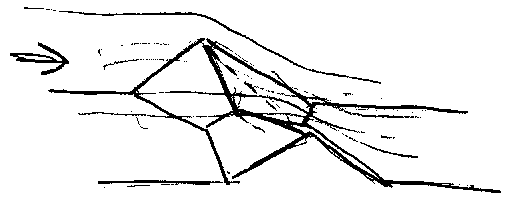
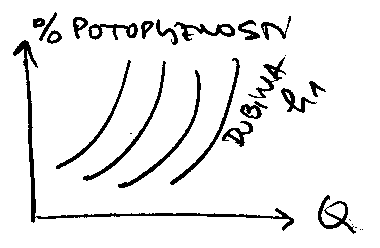 Dosta dobro i jednsotavno objasnjenje potapanja i
suzenja i praga je kod Hajdina, Mehanika fluida II str.106,
sl.106-10
Dosta dobro i jednsotavno objasnjenje potapanja i
suzenja i praga je kod Hajdina, Mehanika fluida II str.106,
sl.106-10
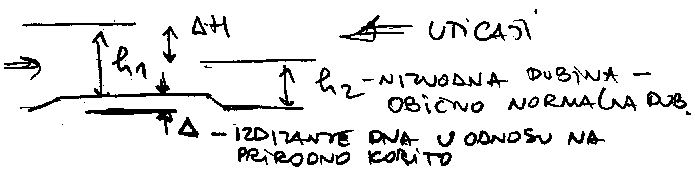
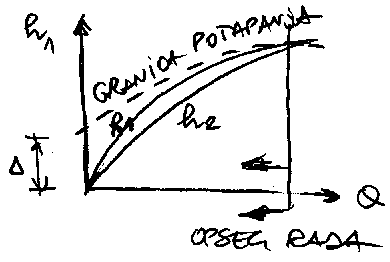 Proveri jos jednom slike, vidi Hajdinovu knjigu
Proveri jos jednom slike, vidi Hajdinovu knjigu

|
(9.6) |
|
|
|
|

|
|
|
|
|
|

|
|
|
|
|
(9.7) |
|

|
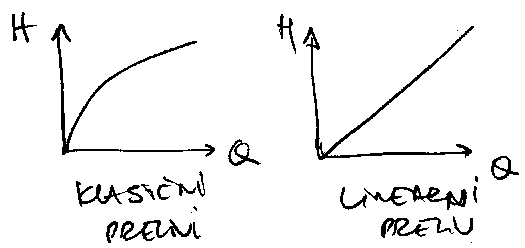
|

|
(9.8) |
|
|
|
|
|
|
|
|
|
|
(9.9) |




 Uzeti par obrazaca iz Ackers-a - prvo ih proveri!
Uzeti par obrazaca iz Ackers-a - prvo ih proveri!
|

|
|
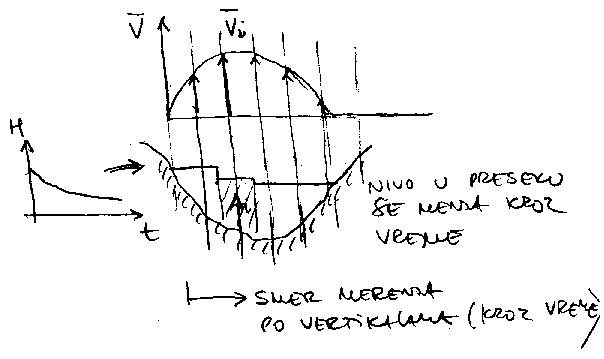
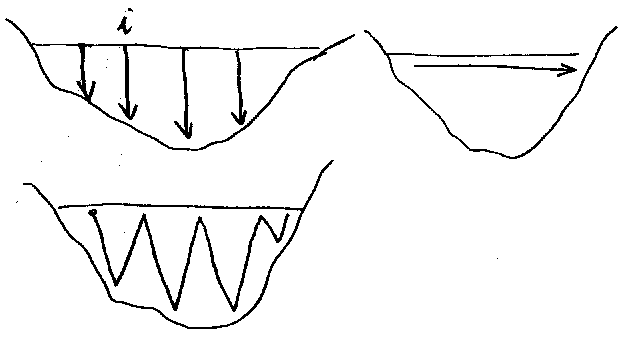
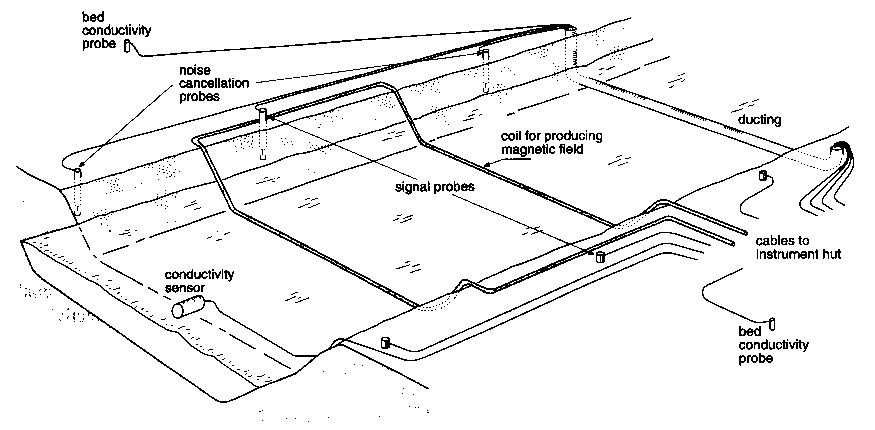 Ili po celom preseku ili index brzine
Ili po celom preseku ili index brzine
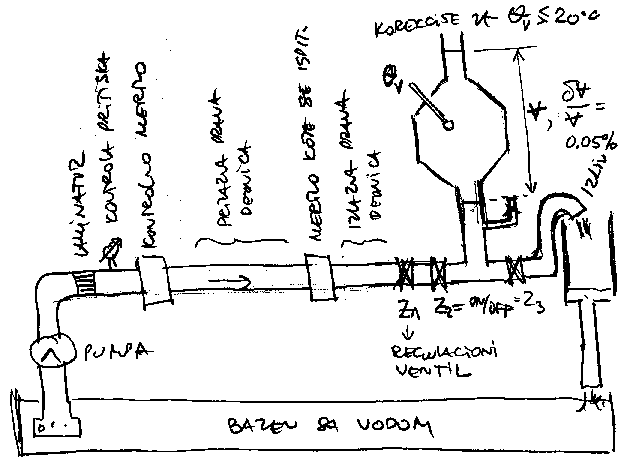
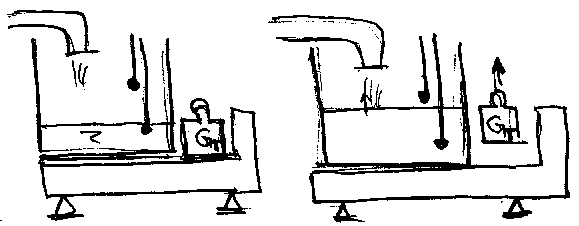
 Svodi se na punjenje poznate zapremine (rezervoar ili slicno - cesto
se pravi velika greska jer se ne zna povrsina kao ni tacni
ulazi-izlazi) ili na primenu pretvaraca za merenje brzine koji se pod
pritiskom postavljaju u cev - insertion type flow meters (hot film, EM
sonde, anubar). Koriste se i UZV meraci, ali sa nizom tacnos\'cu.
Svodi se na punjenje poznate zapremine (rezervoar ili slicno - cesto
se pravi velika greska jer se ne zna povrsina kao ni tacni
ulazi-izlazi) ili na primenu pretvaraca za merenje brzine koji se pod
pritiskom postavljaju u cev - insertion type flow meters (hot film, EM
sonde, anubar). Koriste se i UZV meraci, ali sa nizom tacnos\'cu.
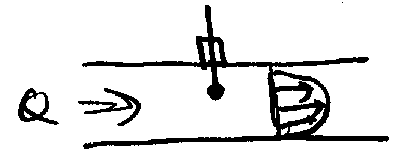

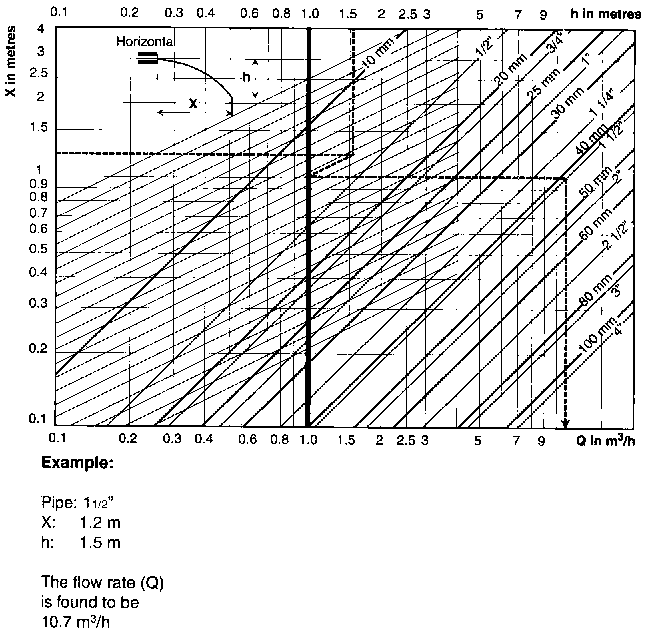 Vidi Grundfos katalog - imam skenirano!
Vidi Grundfos katalog - imam skenirano!

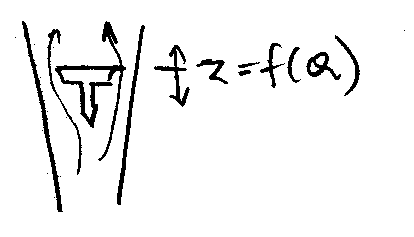
|
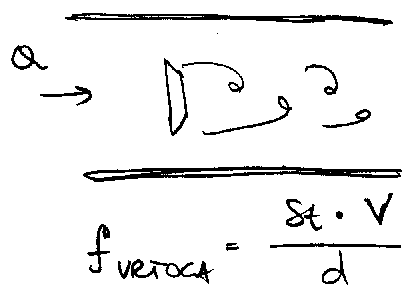 Pogledati knjigu Fluid Mechanics of Flow Metering
(Wolfgang Merzkirch (Editor)) kod mene na
D:\OneDrive\Nastava\MUHA\Knjige-MUHA, posebno poglavlje 6:
Vortex-Shedding Flow Metering Using Ultrasound
Pogledati knjigu Fluid Mechanics of Flow Metering
(Wolfgang Merzkirch (Editor)) kod mene na
D:\OneDrive\Nastava\MUHA\Knjige-MUHA, posebno poglavlje 6:
Vortex-Shedding Flow Metering Using Ultrasound