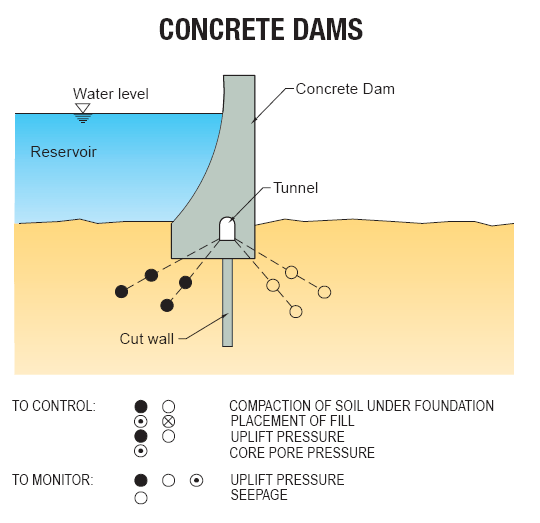
|

|

| Visina | patm |
| [m] | [kPa] |
| (nivo mora) 0 | 101.325 |
| 1500 | 84.8 |
| 3000 | 69.0 |
|

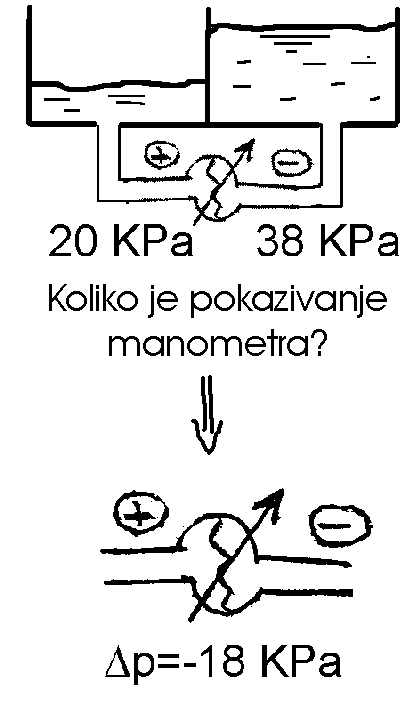

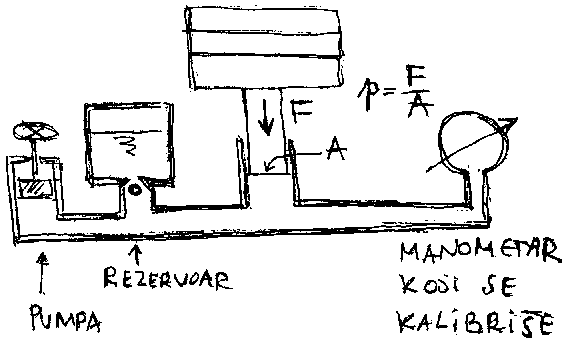
|
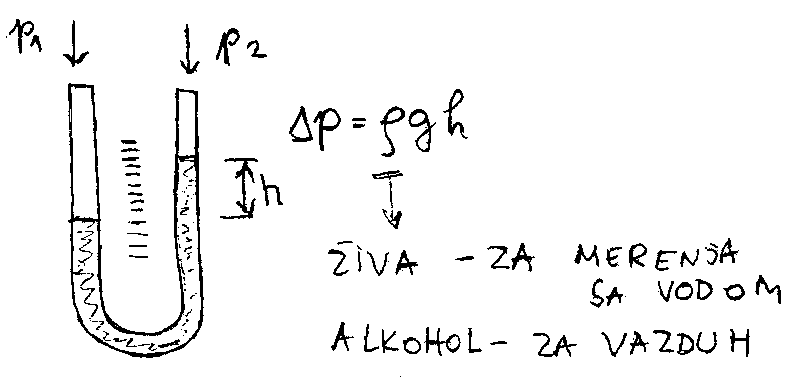

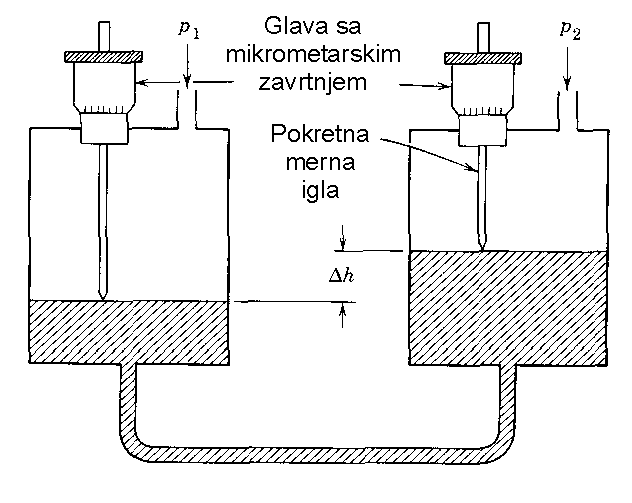
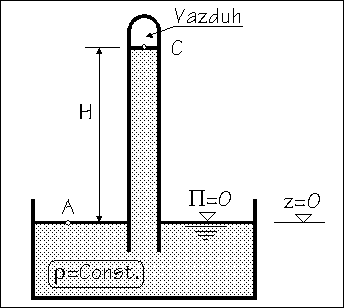
|
|
|
| (6.1) |
|
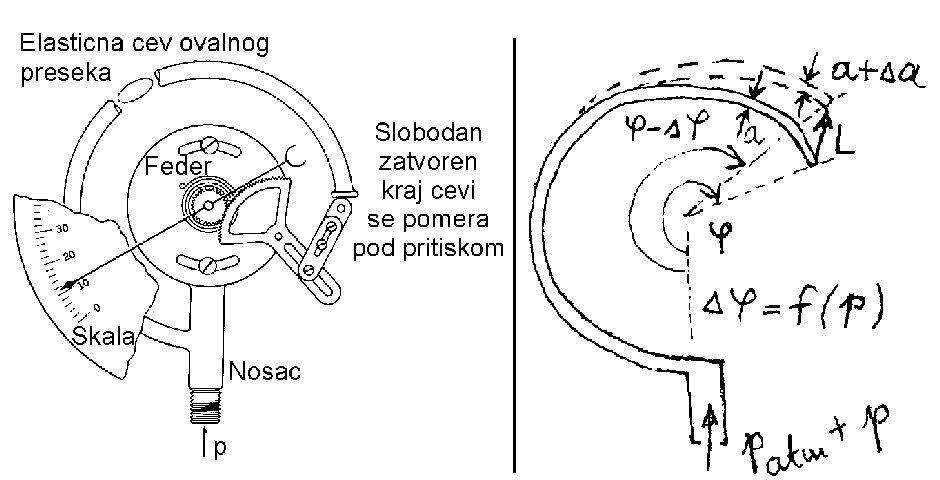
|




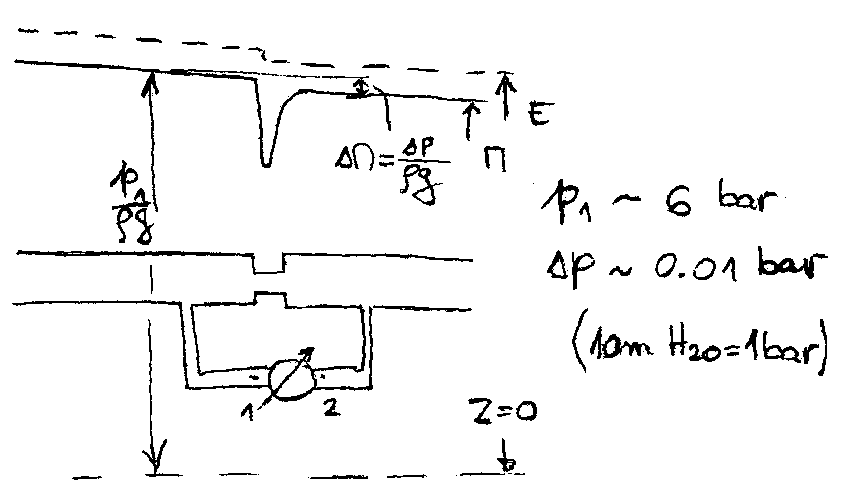

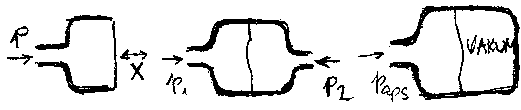

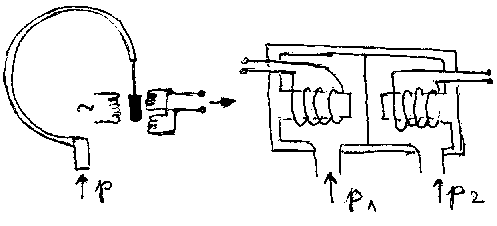

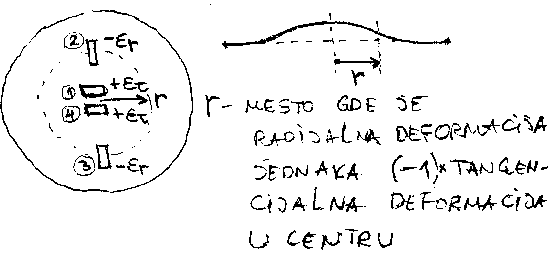
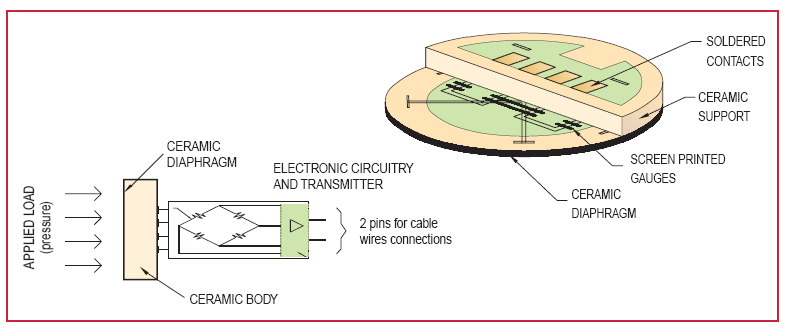
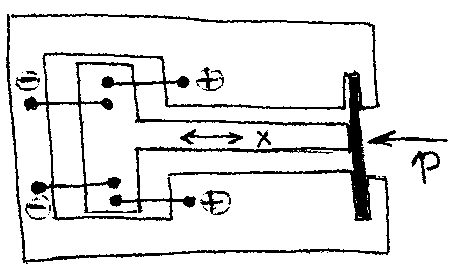
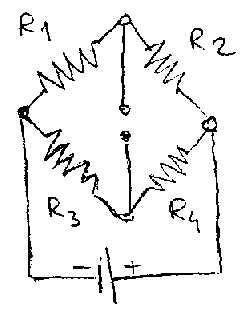 Ako se koristi membrana, njena deformacija se meri pomo\'cu 4 merne trake, tako postavljene da se postigne promena otpornosti DR1 = DR4 = - DR2 = - DR3 , cime se dobija pun Vitstonov most i maksimalna osetljivost sistema, slika 6.23.
Ako se koristi membrana, njena deformacija se meri pomo\'cu 4 merne trake, tako postavljene da se postigne promena otpornosti DR1 = DR4 = - DR2 = - DR3 , cime se dobija pun Vitstonov most i maksimalna osetljivost sistema, slika 6.23.