Kod merenja duzina metrom, usvojen je princip da je merna neodredjenost ±0.5 od najmanje podele na skali. Potrebno je posebnu paznju posvetiti uglu pod kojim se ocitavaju vrednosti na skali: ako je ugao razlicit od 900, pravi se sistematska greska koja pove\'cava neodredjenost. Za preciznija merenja duzine prave se lenjiri sa nonijusom, gde je obezbedjen prav ugao merenja i gde je merna neodredjenost manja od 0.1 mm ili 0.05 mm.
Kod merenja duzina metrom, usvojen je princip da je merna neodredjenost ±0.5 od najmanje podele na skali. Potrebno je posebnu paznju posvetiti uglu pod kojim se ocitavaju vrednosti na skali: ako je ugao razlicit od 900, pravi se sistematska greska koja pove\'cava neodredjenost. Za preciznija merenja duzine prave se lenjiri sa nonijusom, gde je obezbedjen prav ugao merenja i gde je merna neodredjenost manja od 0.1 mm ili 0.05 mm.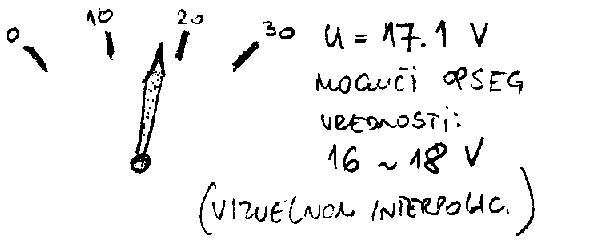 Analogni instrumenti sa kretnim kalemom
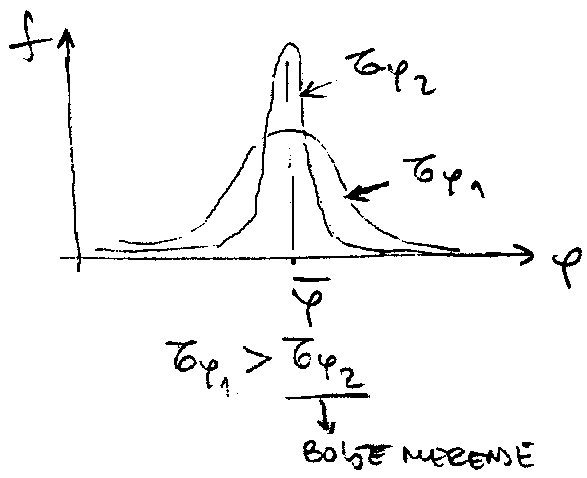
se cesto koriste za merenje velicina koje fluktuiraju. Tada se ostavlja mogu\'cnost operatoru da sam "ceni" srednju vrednost, unose\'ci iskustveno "tezisne koeficijente" tako sto daje ve\'cu tezinu manjim ili ve\'cim vrednostima, u zavisnosti od toga koliko je dugo igla mernog instrumenta bila u kojoj oblasti mernih vrednosti.
Vazno: i sam instrument "laze", pravi gresku koja se izrazava preko "merne klase" - kao procenat greske u odnosu na pun opseg instrumenta: Klase tacnosti kod analognog instrumenta sa kretnim kalemom
Analogni instrumenti sa kretnim kalemom
se cesto koriste za merenje velicina koje fluktuiraju. Tada se ostavlja mogu\'cnost operatoru da sam "ceni" srednju vrednost, unose\'ci iskustveno "tezisne koeficijente" tako sto daje ve\'cu tezinu manjim ili ve\'cim vrednostima, u zavisnosti od toga koliko je dugo igla mernog instrumenta bila u kojoj oblasti mernih vrednosti.
Vazno: i sam instrument "laze", pravi gresku koja se izrazava preko "merne klase" - kao procenat greske u odnosu na pun opseg instrumenta: Klase tacnosti kod analognog instrumenta sa kretnim kalemom
Primer: Kolika je srednja vrednost velicine koju meri instrument? (koristiti linearnu skalu 0-30 V) KLIKNI
Preko Interneta se moze pogledati samo AnimatedGIF verizja
(Primer omogu\'cio svojom dobrotom i nesebicnos\'cu Budimir Miljkovi\'c, poznatiji kao Buda m)
Odgovor potrazite ovde 1. Kao pomo\'c, pogledajte slike vremenskog dijagrama sirovog signala, jednom filtriranog, dva puta filtriranog i tri puta filtriranog signala.
Veliki problem analognih instrumenata sa kazaljkom je postojanje razmaka izmedju kazaljke i skale instrumenta. Da bi se obezbedio prav ugao pod kojim se gleda skala, obicno se postavlja iza kazaljke malo ogledalo: operator mora da prilikom ocitavanja skale "poklopi" kazaljku i njen lik u ogledalu.
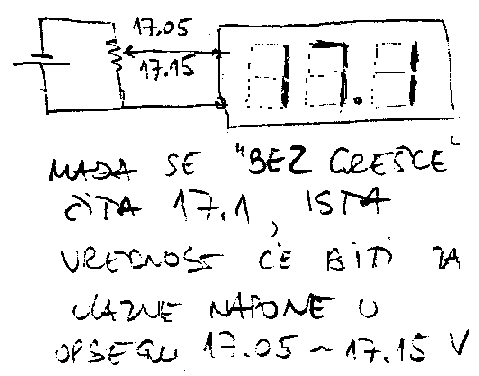 Na slici 2.4 je prikazan digitalni voltmetar, koji meri napon na klizacu potenciometra, sa rezolucijom od jedne decimale. Za sve ulazne napone u opsegu od 17.04999 V do 17.14999 V, voltmetar \'ce pokazivati istu vrednost: 17.1 V. Neodredjenost ocitavanja voltmetra je ±0.05 V, ili ±0.5 od zadnje prikazane cifre.
Tacnost digitalnog instrumenta, medjutim, nije isto sto i rezolucija. Tacnost je po pravilu niza od navedene merne neodredjenosti, i ukljucuje nelinearnost analognog pojacavackog dela, nelinearnost i greske u analogno - digitalnoj konverziji, kao i greske u referentnom naponu.
Na slici 2.4 je prikazan digitalni voltmetar, koji meri napon na klizacu potenciometra, sa rezolucijom od jedne decimale. Za sve ulazne napone u opsegu od 17.04999 V do 17.14999 V, voltmetar \'ce pokazivati istu vrednost: 17.1 V. Neodredjenost ocitavanja voltmetra je ±0.05 V, ili ±0.5 od zadnje prikazane cifre.
Tacnost digitalnog instrumenta, medjutim, nije isto sto i rezolucija. Tacnost je po pravilu niza od navedene merne neodredjenosti, i ukljucuje nelinearnost analognog pojacavackog dela, nelinearnost i greske u analogno - digitalnoj konverziji, kao i greske u referentnom naponu.
Primer: isecak iz kataloga jednog proizvodjaca sonde za nivo vode pokazuje ociglednu razliku izmedju specifikacija o rezoluciji i ukupnoj tacnosti. Evo jos jedan primer
Digitalni voltmetri su prakticni kada se mere relativno staticne velicine. Ako merna velicina fluktuira, tada je teze na njima proceniti mernu vrednost KLIKNI (ako ne radi link, otvori rucno Metex.exe u ProgramFiles-u
(Preko Interneta se moze pogledati samo slika instrumenta)
|
Na primer, u kalibracionom certifikatu Hydreka EM sondi, stoji da je kao etalonsko merilo za protok koris\'ceno 4 EM merila postavljena na red (jedan iza drugog), svaki klase 0.2%. Ukupno, ocekivana klasa merenja je:
|
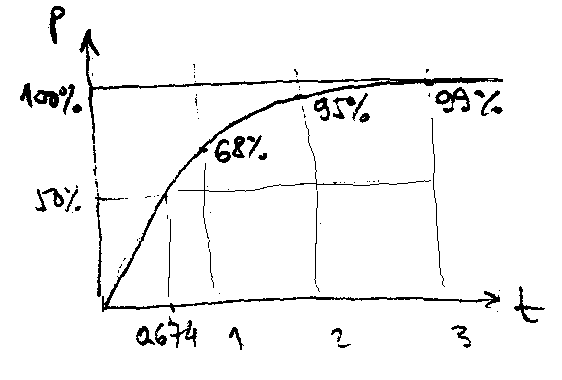
 Da bi ponovljena merenja mogla da se uporedjuju, neophodno je obezbediti ponovljivost eksperimenta: treba da budemo sigurni da u svakom eksperimentu merimo istu velicinu pod istim uslovima.
Na slici 2.5 je prikazan sistem za merenje protoka sa dva merila na jednoj dugackoj cevi. Na zalost, uslovi merenja nisu isti, pa nije mogu\'ce koristiti srednju vrednost protoka (nisu isti prilazni uslovi, neustaljenost u toku, ...). Ovo je posebno znacajno pri izradi bilansa protoka na nekom sistemu!
Da bi ponovljena merenja mogla da se uporedjuju, neophodno je obezbediti ponovljivost eksperimenta: treba da budemo sigurni da u svakom eksperimentu merimo istu velicinu pod istim uslovima.
Na slici 2.5 je prikazan sistem za merenje protoka sa dva merila na jednoj dugackoj cevi. Na zalost, uslovi merenja nisu isti, pa nije mogu\'ce koristiti srednju vrednost protoka (nisu isti prilazni uslovi, neustaljenost u toku, ...). Ovo je posebno znacajno pri izradi bilansa protoka na nekom sistemu!
 Primer neizbeznosti greske:
Primer neizbeznosti greske:
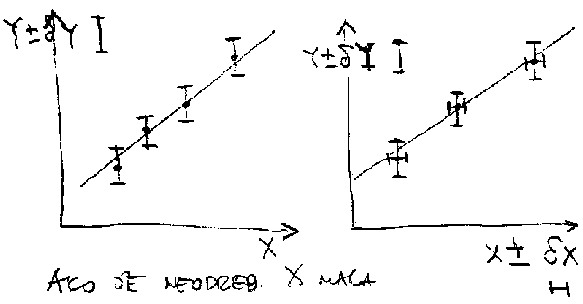 Merene vrednosti i neodredjenost se mogu prikazati i graficki. Na slici 2.6 je na levoj strani prikazan slucaj kada je neodredjenost nezavisne velicine X za red velicine manja od zavisne velicine Y, dok je na desnoj strani primer kada su merne neodredjenosti istog reda velicine.
Merene vrednosti i neodredjenost se mogu prikazati i graficki. Na slici 2.6 je na levoj strani prikazan slucaj kada je neodredjenost nezavisne velicine X za red velicine manja od zavisne velicine Y, dok je na desnoj strani primer kada su merne neodredjenosti istog reda velicine.
 Ako su greske u merenju duzina h i b samo slucajne, tada se:
Ako su greske u merenju duzina h i b samo slucajne, tada se: