Годишњи задатак на предмету

“Мерења у хидротехници”

 

 

          

            Мерење протока у

          отвореним каналима

         помоћу бочног сужења

 

 

 

Професор : Доцент Др Душан M. Продановић, дипл. инж.

 Асистент  : Немања Бранисављевић

 

 Студенти  :  Глишић Иван

                      Војт Предраг

                      Радовић Ђорђе

 

 

                                                                         Јануар. 2006 год.

Годишњи задатак из предмета “Мерења у хидротехници”

 

 

У оквиру годишњег задатка требало је да се обави следеће:

 

1. Анализира литература   -   разни типови сужења

-  услови за рад мерног уређаја

-  утицај низводне дубине

 

2. Обави мерења на лабораторијском каналу

-         користити полу-сужење

-         дубине мерити помоћу мерне игле

-         одредити коефицијент протока C_Q у устаљеним условима

-         анализирати утицај низводних услова

-         анализирати утицај долазних услова

 

3. Израда математичког модела у MatLab-u. Предвидети коришћење различите геометрије у долазном и у суженом пресеку, као и могућност потапања са низводне стране

 

4. Израде капацитивне сонде за мерење нивоа, линеаризују их и калибришу.

 

5. Одредити грешку мерења протока у функцији протока, помоћу направљеног мерног система узимајући Томпсонов прелив као референтно мерило. Грешку одредити за различите степене потопљености сужења.

 

 

 

 

1. АНАЛИЗА ЛИТЕРАТУРЕ

Изршена је анализа следеће литературе:

       -   Мерни објекти за одређивање протицаја у отвореним токовима (Г. Хајдин) 

       -   Објекти за одређивање протицаја у отвореним каналима 

              (Завод за хидротехнику  ГФ Београд)

 -   Discharge measurement structures (Working group on small hidraulic structures)

 -   Wiers and flumes for flow measurement (P. Ackers, W. R. White,

               J. A. Perkins, J. M. Harrison)

 

Анализирана су претходна искуства на различитим типовима сужења, Parshall-ово сужење, Rectangular сужење, Trapezoidal сужење, U сужење. Из литературе се могу наћи препоручене димензије објекта, при чему треба задовољити непотапање објекта и уклопити неопходно подизање нивоа узводно од сужења. Дошли смо до следећих закључака:

- неопходно је да дно мерног канала буде хоризонтално

- узводно од сужења је неопходан миран режим

- препоручује се непотопљено течење у сужењу (јер у том случају, проток  меримо само помоћу узводне дубине и мања је грешка у мерењу протока)

            - у случају потопљеног течења проток се мери помоћу узводне и низводне дубине, при чему је и већа грешка у одређивању протока

            - ако је узводно од сужења буран режим, он може да се умири и помоћу различитих препрека у самом току узводно од сужења

            - пожељно је да канал заједно са сужењем буде хидраулички обликован, како улазни део, тако и излазни део канала

 

ЗАКЉУЧАК: Неопходно је да хидротехничар прорачуна утицај сужења

 

 

 

2. ЛАБОРАТОРИЈСКА МЕРЕЊА

Мерно сужење на ком смо ми мерили је несиметрично полу сужење са следећим димензијама:

 

 

 

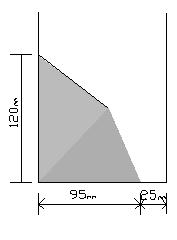
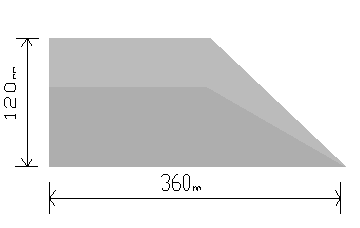
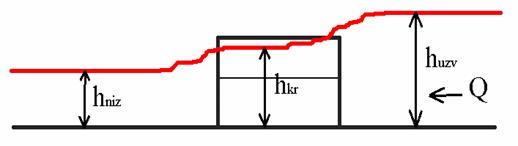
Дубине су мерене помоћу мерне игле на три профила: узводно од сужења, у сужењу и низводно од сужења. Проток је мерен помоћу Томпсоновог прелива.

На основу лабораторијских мерења одредили смо коефицијент протока  C_Q за непотопљено течење на следећи начин. За различите вредности протока и дубина (које су измерене помоћу мерне игле за одговарајући проток), постављена је енергетске једначине између профила узводно од сужења и у самом сужењу.

 

Мора да се уведе корекција протока, јер флуид није идеалан. За неки реалан флуид мора да се уведе коеицијент протока C_Q:

 

Q_REALNO=C_Q×Q_IDEALNO

 

За познату вредности протока и њему одговарајућих измерених дубина,  помоћу постављене енергетске једначине и корекције протока са коефицијентом C_Q  добија се одређена вредност коефицијента C_Q. Варирајући различите вредности протока добијају се различите вредности C_Q. Њиховим осредњавањем добија се да је коефицијент C_Q =0.96.

 

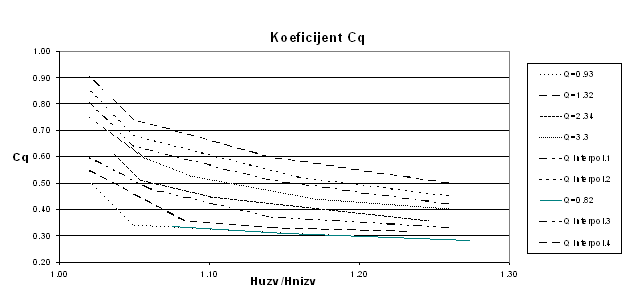
За потопљено течење коефицијент C_Q више није константа, већ зависи од протока, низводних и узводних дубина. Енергетска једначина се поставља између профила узводно и низводно од сужења. Добијају се криве C_Q:

 

Проблем је био наћи границу потопљености. На основу резултата мерења усвојено је да је за односе h_uzv/h_nizv веће од 1.26 течење у сужењу непотопљено, а за односе мање од 1.26 течење у сужењу је потопљено.

 

3.МАТЕМАТИЧКИ МОДЕЛ

Урађен је математички модел у MatLab-u. У MatLab-u су направљени фајлови (profilniz.txt, profilsuz.txt, profiluzv.txt) у које се убаце подаци о геометрији попречних пресека. Главни програм се у току рада позива на потпрограм “Parametri.m” који служи за прорачун карактеристика попречних пресека, а потпрограм се позива на фајлове у којима се налазе подаци о геометрији попречних пресека. У наредби Function са којом се позива потпрограм уноси се дубина h и профил који се тражи, а добија се површина  A и ширина воденог огледала B. У програм се унесу узводна и низводна дубина (h_uzv и h_nizv), а у зависности од њиховог односа h_uzv/h_nizv програм рачуна са одговарајућим алгоритмом (потопљено или непотопљено течење). Главни програм, потпрограм, као и подаци о профилима су дати на крају у прилогу годишњег задатка

 

 

 

4.МЕРЕЊЕ НИВОА КАПАЦИТИВНИМ СОНДАМА

Урађене су две капацитивне сонде. Њихова улога је да у зависности од промене нивоа воде у каналу, оне мењају своју капацитивност. Помоћу те промене капацитивности, електроника која је монтирана на главе сонди, ту промену капацитивности претвара у фреквенцију коју после претварамо у вредност дубине воде у каналу.

              Прво смо пробали да урадимо капацитивне сонде помоћу лимених профила и лакиране бакарне жице. Проблем је био са жицом јер је била осетљива на механичка оштећења и није било могуће да се изврши калибрација сонди, јер је жица у току мерења мењала своје карактеристике. Тада смо направили капацитивне сонде помоћу тефлонске жице која је показала задовољавајуће резултате. “Тачан” ниво воде је мерен мерном иглом.

 

 

 

                                     Скица сонде

 

           

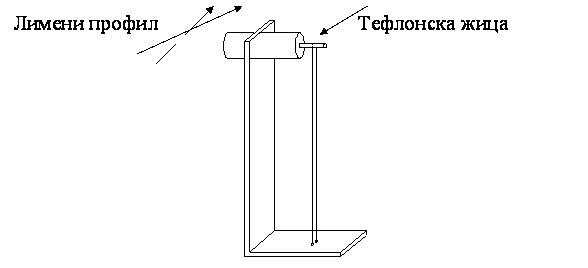
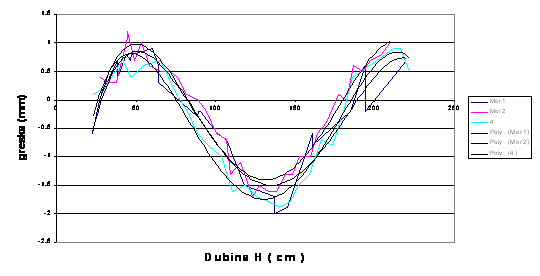
На графику је дато њихово одступање од вредности по дубини, добијених помоћу мерне игле за три мерења.

 

 

 

 

5.ГРЕШКЕ ПРИ МЕРЕЊУ ПРОТОКА.

Одступање мерене дубине помоћу сонди од стварне (дубина измерена помоћу мерне игле) је у распону ±1.5mm, али се грешка може кориговати апроксимацијом полиномом четвртог степена. Тада је грешка у распону ±0.5mm.

За апсолутно тачне вредности мерења смо усвојили очитавања на мерној игли.

Проблем код очитавања са мерном иглом је био таласање воде, па је могућа грешка при очитавању била ±0.5mm. Утицај те грешке на одређивање протока, за различите вредности протока за непотопљено течење је дат на следећем графику:

 

ПРИЛОГ:   

 

                                  ГЛАВНИ ПРОГРАМ

 

clear all

Qmer=1;

huzv=7.43

hniz=5.2

hh=huzv/hniz;

if hh>1.26;

  h=huzv/100;

  cq=0.96;%uneti cq

  profil=load('profiluzv.txt');

  pom=parametri(h,profil);

  a=pom(1,1);

  b=pom(1,2);

  hsuz=(h-h/10)/2+h/10;

  r=1;

  hmin=h/10;

  hmax=h;

    while r>0.000001;

      profil=load('profilsuz.txt');

      pom=parametri(hsuz,profil);

      asuz=pom(1,1);

      bsuz=pom(1,2);

      qsuz=sqrt(9.81*asuz^3/bsuz);

      r=qsuz-cq*asuz*sqrt(19.62*(h-hsuz)+qsuz^2/a^2);

      deltah=(hmax-hmin)/2;

        if r>0;

          hmax=hsuz;

          hmin=hsuz-deltah;

          hsuz=hsuz-deltah/2;

            else;

              hmin=hsuz;

              hmax=hsuz+deltah;

              hsuz=hsuz+deltah/2;

          end;

              r=abs(r);

          end;      

else

end

if hh<=1.26

     auzv=12*huzv;%cm^2

     aniz=12*hniz;%cm^2

     q=sqrt(9.81*0.12^2*(hniz/100)^3);%m^3/s

     rkk=1;

     hh=huzv/hniz;

        if huzv>16.5;

           Cq=3.4392*hh^2-9.0873*hh+6.49;%huz=18

        else;

           if huzv>14.25;

               Cq=3.5931*hh^2-9.3952*hh+6.5836;%huz=15

           else;

              if huzv>12.93;

                 Cq=3.3069*hh^2-8.6865*hh+6.115;%huz=13.5

              else;

                 if huzv>11.48;

                     Cq=5.0765*hh^2-12.687*hh+8.3275;%huz=12.35

                 else;

                     if huzv>9.96;

                         Cq=4.193*hh^2-10.45*hh+6.8682;%huz=10.61

                     else;

                         if huzv>8.63;

                             Cq=1.4583*hh^2-3.8333*hh+2.8448;%huz=9.3

                         else;

                             if huzv>7.31;

                                 Cq=1.9651*hh^2-4.8326*hh+3.2856;%huz=7.96

                             else;

                                 Cq=0.4242*hh^2-1.2462*hh+1.1809;%huz=6.65

                             end;

                         end;

                     end;

                 end;

             end;

         end;

     end;

    

   

   rkk=1;

    while rkk>0.00001;

        rkk=q-Cq*aniz/10000*sqrt(19.62*(huzv-hniz)/100+q^2/(auzv/10000)^2);

        if rkk>0;

            q=q-0.000004;

        else;

            q=q+0.000004;

        end;

        rkk=abs(rkk);

    end;

end;

odnos_dubina=hh

if hh>1.26

    'Tecenje je nepotopljeno'

    q=qsuz;

else

    'Tecenje je potopljeno'

    q;

end;

Q=q*1000

Greska_u_procentima=(abs(Q-Qmer))/Qmer*100

 

 

ПОТПРОГРАМ ЗА РАЧУНАЊЕ

КАРАКТЕРИСТИКА ГЕОМЕТРИЈСКОГ ПРОФИЛА

 

 

function [ a ] = parametri( h,profil );

%unosi se h i profil( u obliku profil=[x1 z1;x2 z2;xi zi])

%  vracaju se funkcije "a" (povrsina poprecnog preseka) i "b" (sirina

%  vodenog ogledala

m=length(profil);

for i=1:m;

    tackex(i)=profil(i,1);

    tackez(i)=profil(i,2);

end;

a1=0;

z=min(tackez)+h;

    for n=1:m;

        if tackez(n)<z;

            if tackez(n-1)>=z %prvi trougao;

                if tackez(n)~=tackez(n-1);

                    a1=(tackex(n)-tackex(n-1))/abs(tackez(n)-tackez(n-1))*(abs(tackez(n)-z))^(2)/2+a1;

                    x1=tackex(n)-(tackex(n)-tackex(n-1))/(abs(tackez(n)-tackez(n-1)))*abs(tackez(n)-z);

                else;

                    x1=tackex(n);

               end;

            end;

            if tackez(n+1)>=z %poslednji trougao;

                if tackez(n)~=tackez(n+1);

                    a1=(tackex(n+1)-tackex(n))/abs(tackez(n)-tackez(n+1))*(abs(tackez(n)-z))^(2)/2+a1;

                    x2=tackex(n)+(tackex(n+1)-tackex(n))/(abs(tackez(n)-tackez(n+1)))*abs(tackez(n)-z);

                else;

                    x2=tackex(n);

                end;

            else %trapezi izmedju;

                a1=(tackex(n+1)-tackex(n))*(2*z-tackez(n)-tackez(n+1))/2+a1;

            end;

        end;

    end;

    b=x2-x1;

    a=[a1 b];

 

 

 

ГЕОМЕТРИЈА ПОПРЕЧНИХ ПРОФИЛА