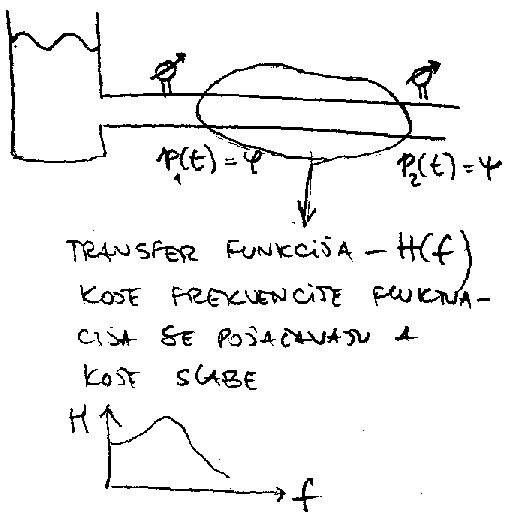
- Meri se HN ( t ) i UA ( t ) .
- Tecenje u cevi je turbulentno (Reynolds-ov broj Re>>2500).
- Koriste se sonde za brzinu i nivo koje registruju brze promene.
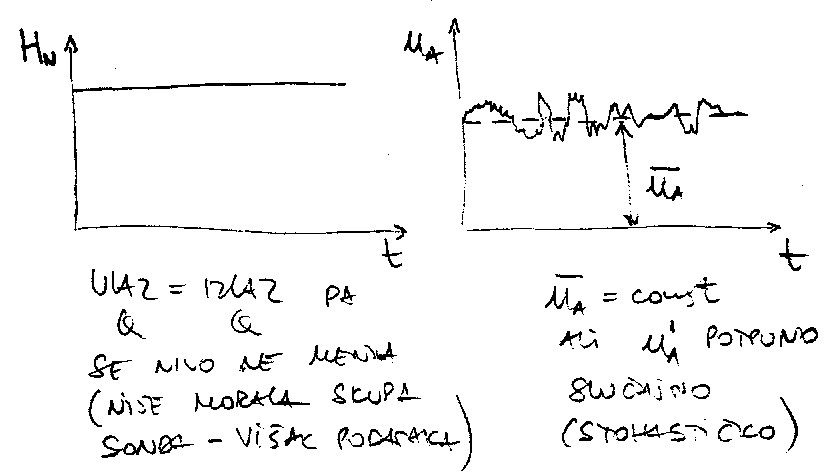
 Primer periodicnih oscilacija: nivo u rezervoaru, odnosno fluktuacije nivoa, HN′( t ) mozemo da racunamo, prate analiticku zavisnost, imaju deterministicki karakter (slika 3.4 levo).
Primer periodicnih oscilacija: nivo u rezervoaru, odnosno fluktuacije nivoa, HN′( t ) mozemo da racunamo, prate analiticku zavisnost, imaju deterministicki karakter (slika 3.4 levo).
Na deterministicki sinusni oblik signala brzine vode u cevi (koji malo kasni u odnosu na nivo), medjutim, dodata je i stohasticka komponenta (slika 3.4 desno) koja je posledica turbulencije i neujednacenosti duvanja vetra.
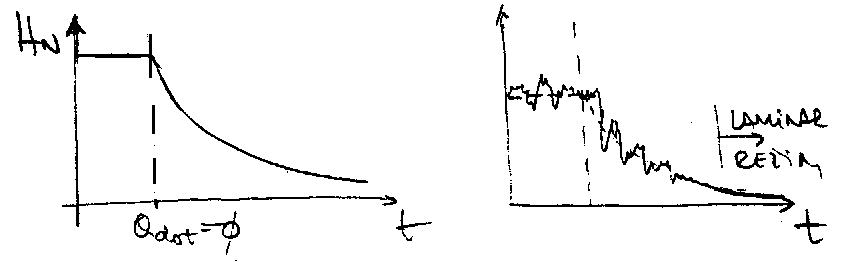 Na levom delu slike 3.5 je prikazan slucaj gde pad nivoa u rezervoaru odgovara onome sto se moze sracunati primenom osnovnih jednacina Hidraulike, pojava je deterministicka. Na desnom delu slike 3.5 je osnovnom deterministickom signalu superponirana slucajna, stohasticka komponenta (obratiti paznju na to da \'ce se zajedno sa brzinom smanjivati i Reynolds-ov broj, pa \'ce u odredjenom trenutku tecenje postati laminarno - nesta\'ce stohasticka komponenta brzine).
Na levom delu slike 3.5 je prikazan slucaj gde pad nivoa u rezervoaru odgovara onome sto se moze sracunati primenom osnovnih jednacina Hidraulike, pojava je deterministicka. Na desnom delu slike 3.5 je osnovnom deterministickom signalu superponirana slucajna, stohasticka komponenta (obratiti paznju na to da \'ce se zajedno sa brzinom smanjivati i Reynolds-ov broj, pa \'ce u odredjenom trenutku tecenje postati laminarno - nesta\'ce stohasticka komponenta brzine).

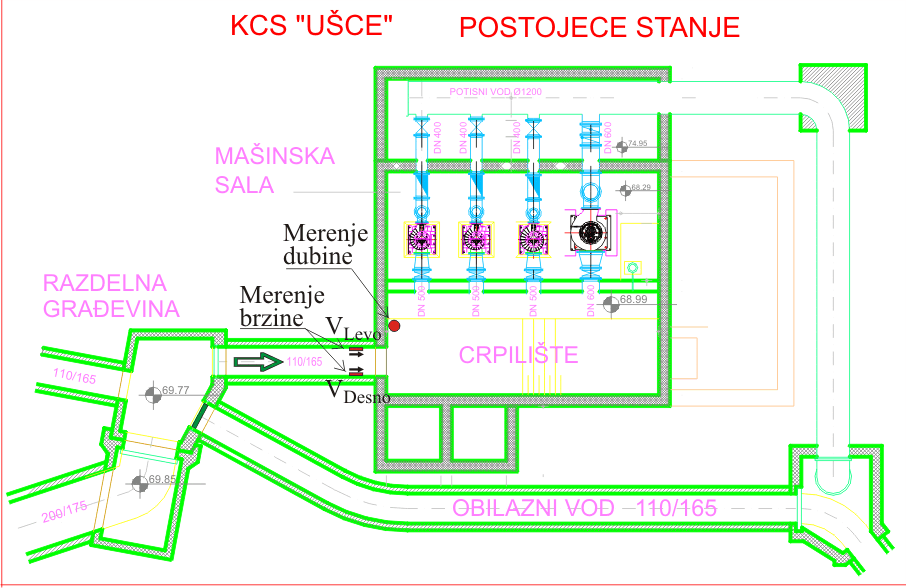 Na ulazu u crpiliste je postavljen sistem za merenje protoka, koji meri brzine na levom i desnom boku dovodnog kolektora i nivo u crpnom bazenu. Ako se pogleda dijagram izmerenih protoka u nekom intervalu, moze se pogresno zakljuciti da je stohastiska komponenta velika:
Na ulazu u crpiliste je postavljen sistem za merenje protoka, koji meri brzine na levom i desnom boku dovodnog kolektora i nivo u crpnom bazenu. Ako se pogleda dijagram izmerenih protoka u nekom intervalu, moze se pogresno zakljuciti da je stohastiska komponenta velika:
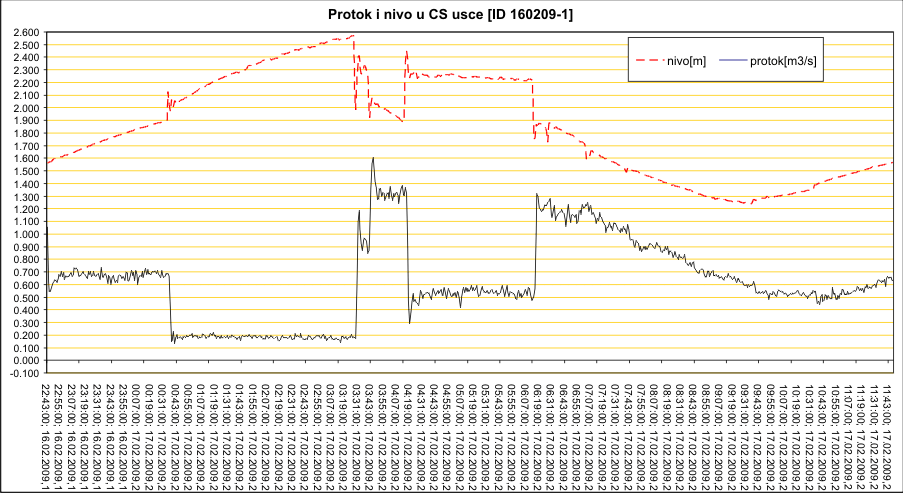
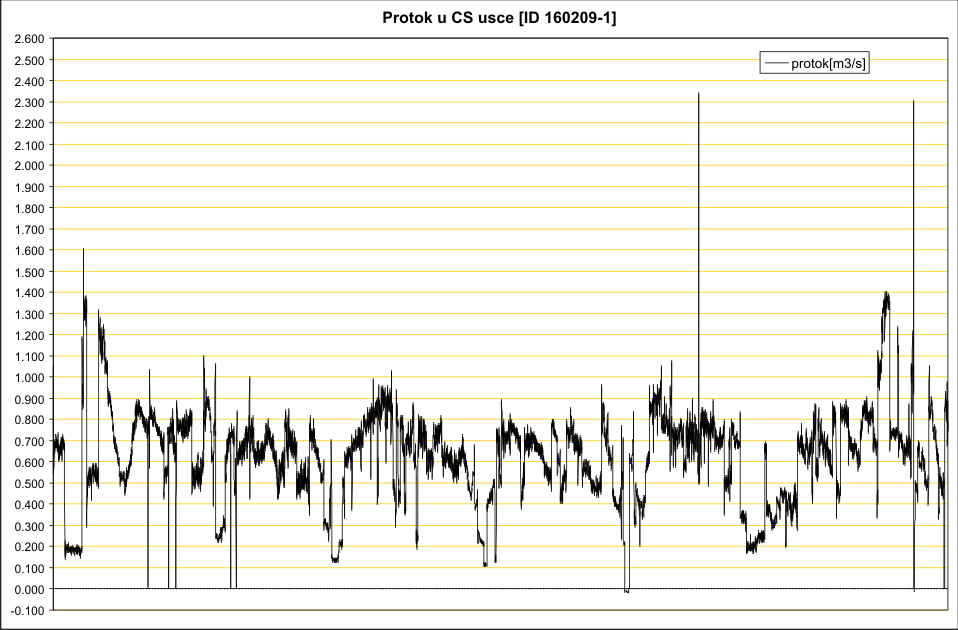 Medjutim, ako se zumira samo poslednji dan, i ako se nacrtaju nivoi u crpnom bazenu, mogu se lepo uociti periodi kada rade pumpe i kada su iskljucene, sto cini determinsticku komponentu varijacije protoka. Stohasticka komponenta su samo fluktuacije protoka oko srednje vrednosti.
Medjutim, ako se zumira samo poslednji dan, i ako se nacrtaju nivoi u crpnom bazenu, mogu se lepo uociti periodi kada rade pumpe i kada su iskljucene, sto cini determinsticku komponentu varijacije protoka. Stohasticka komponenta su samo fluktuacije protoka oko srednje vrednosti.
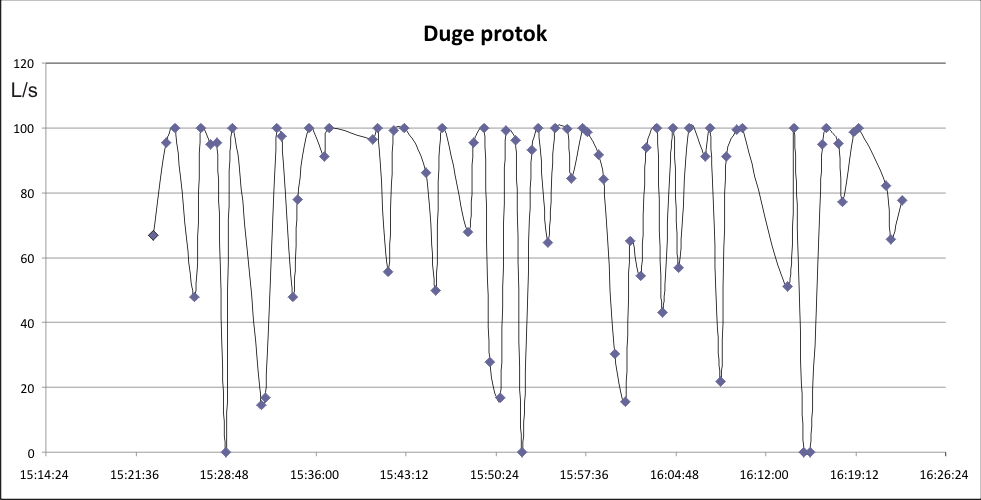 Pregledom dijagrama, vidi se da se protok u roku od par sekundi smanjuje sa 100 L/s na 0L/s i opet vra\'ca na istu vrednost. Takve promene bi mogle da ukazu na slede\'ce:
Pregledom dijagrama, vidi se da se protok u roku od par sekundi smanjuje sa 100 L/s na 0L/s i opet vra\'ca na istu vrednost. Takve promene bi mogle da ukazu na slede\'ce:
 Na slici 3.10 je data sematski podela deterministickih velicina. U nastavku teksta se svaka od velicina detaljnije obradjuje.
Na slici 3.10 je data sematski podela deterministickih velicina. U nastavku teksta se svaka od velicina detaljnije obradjuje.
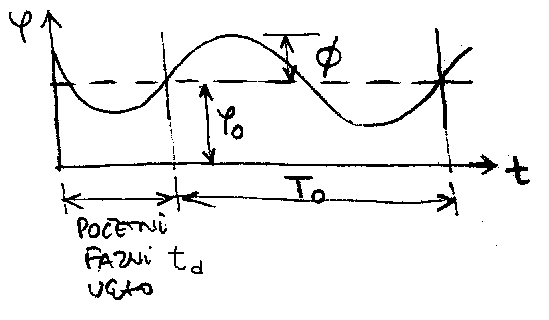
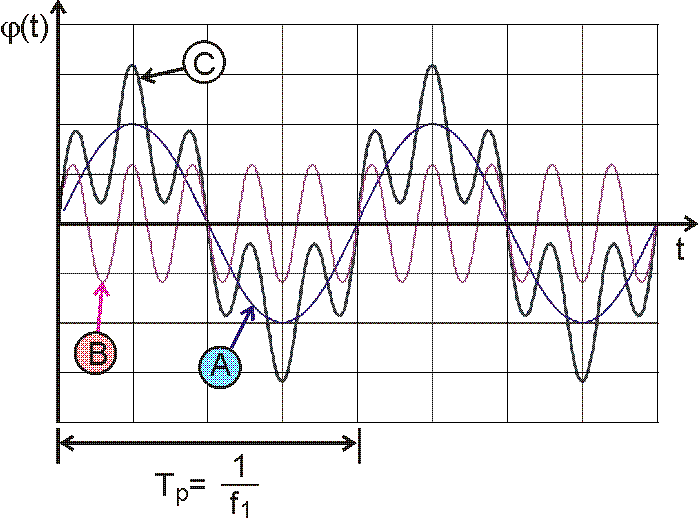
 Graficki, velicina φ( t ) se moze predstaviti kroz vreme (slika 3.11),
ili u formi diskretnog spektra, kao zavisnost amplitude signala od frekvencije (slika 3.12).
Graficki, velicina φ( t ) se moze predstaviti kroz vreme (slika 3.11),
ili u formi diskretnog spektra, kao zavisnost amplitude signala od frekvencije (slika 3.12).
 NAPOMENA: Za prikaz razlicitih signala, zbir dva signala i njihovu furijeovu transformaciju kao i auto i kros korelaciju, mozete koristiti MatLab program FURIJE
- preuzmite sa sajta ZIP file RazniSignali.zip i raspakujte .M i .FIG fileove u isti direktorijum.
Ekran programa na kome se vidi zbir dve sinusoide frekvencija f i 3f (cetvrtka je u stvari zbir sinusoida frekvencija f, 3f, 5f, 7f...)
NAPOMENA: Za prikaz razlicitih signala, zbir dva signala i njihovu furijeovu transformaciju kao i auto i kros korelaciju, mozete koristiti MatLab program FURIJE
- preuzmite sa sajta ZIP file RazniSignali.zip i raspakujte .M i .FIG fileove u isti direktorijum.
Ekran programa na kome se vidi zbir dve sinusoide frekvencija f i 3f (cetvrtka je u stvari zbir sinusoida frekvencija f, 3f, 5f, 7f...)


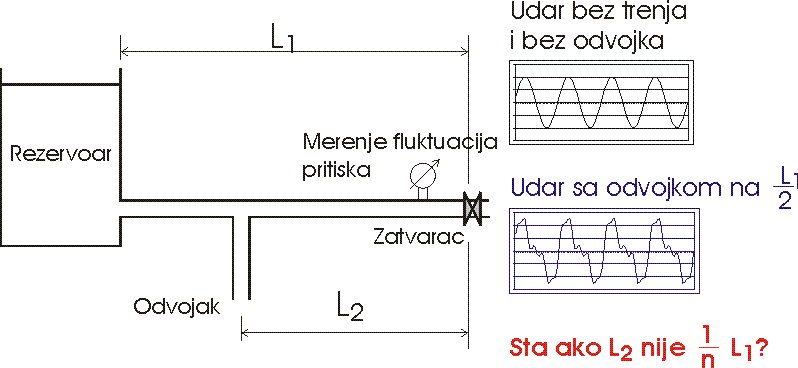


 Analiticki, prelazna neperiodicna velicina se moze izraziti:
Analiticki, prelazna neperiodicna velicina se moze izraziti:
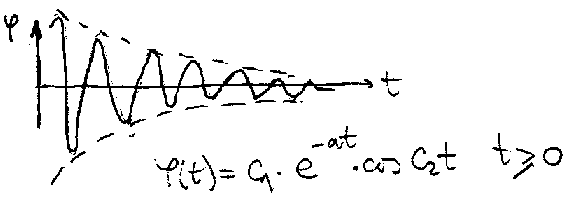
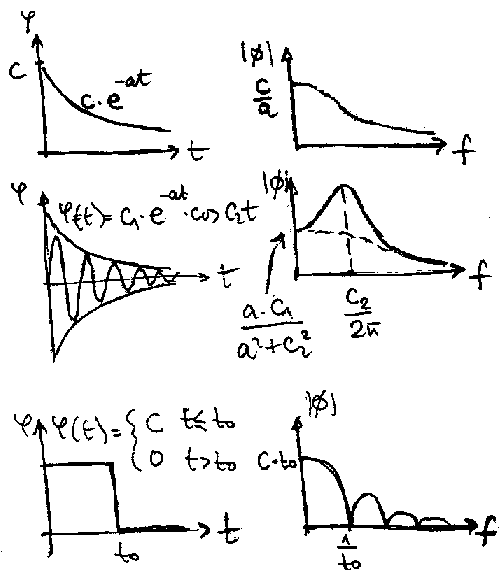
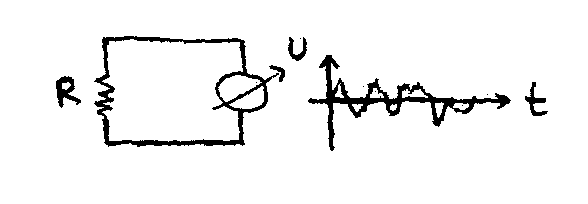 S obzirom na stohasticnost, u analizi se koristi matematicka statistika. Bitno je prvo prepoznati kojoj grupi pojava neka velicina pripada, jer se primenjuju razliciti statisticki aparati.
S obzirom na stohasticnost, u analizi se koristi matematicka statistika. Bitno je prvo prepoznati kojoj grupi pojava neka velicina pripada, jer se primenjuju razliciti statisticki aparati.


 Sve rezultate merenja ("iseckan" dugacak niz ili visestruko merenje) mozemo presloziti (nacrtati) tako da pocinju od istog trenutka (slika 3.25).
Sve rezultate merenja ("iseckan" dugacak niz ili visestruko merenje) mozemo presloziti (nacrtati) tako da pocinju od istog trenutka (slika 3.25).
 Za tako dobijene (ili preslozene) rezultate merenja mozemo racunati statisticke pokazatelje u vremenu (t) kroz ceo skup {φ(t)}.
Za tako dobijene (ili preslozene) rezultate merenja mozemo racunati statisticke pokazatelje u vremenu (t) kroz ceo skup {φ(t)}.
 Nacin kako se mogu meriti
Nacin kako se mogu meriti  Merenje efektivne vrednosti velicine φ je analognim instrumentima prilicno komplikovano, pa su takvi uredjaji po pravilu dosta skupi.
Merenje efektivne vrednosti velicine φ je analognim instrumentima prilicno komplikovano, pa su takvi uredjaji po pravilu dosta skupi.
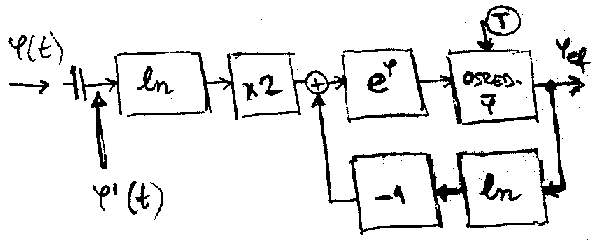

 Vreme u kome je signal u opsegu φ, φ+ ∆φ:
Vreme u kome je signal u opsegu φ, φ+ ∆φ:
 Na slici 3.33 su dati primeri nekih signala sa odgovaraju\'cim funkcijama gustine verovatno\'ce. Iz primera se vidi jedna od osnovnih primena funkcije gustine verovatno\'ce - da se proveri postojanje periodicnih signala unutar suma, kao i postojanje drugih nelinearnih efekata8.
Na slici 3.33 su dati primeri nekih signala sa odgovaraju\'cim funkcijama gustine verovatno\'ce. Iz primera se vidi jedna od osnovnih primena funkcije gustine verovatno\'ce - da se proveri postojanje periodicnih signala unutar suma, kao i postojanje drugih nelinearnih efekata8.

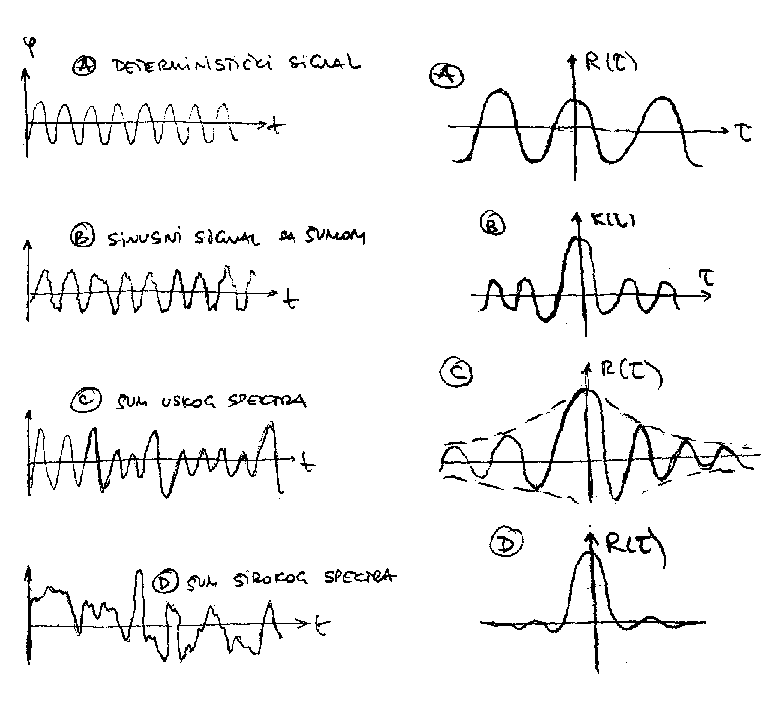 Na slici 3.35 je dat rezultat autokorelacione analize za signale date na slici 3.33. Komentar ...
Na slici 3.35 je dat rezultat autokorelacione analize za signale date na slici 3.33. Komentar ...

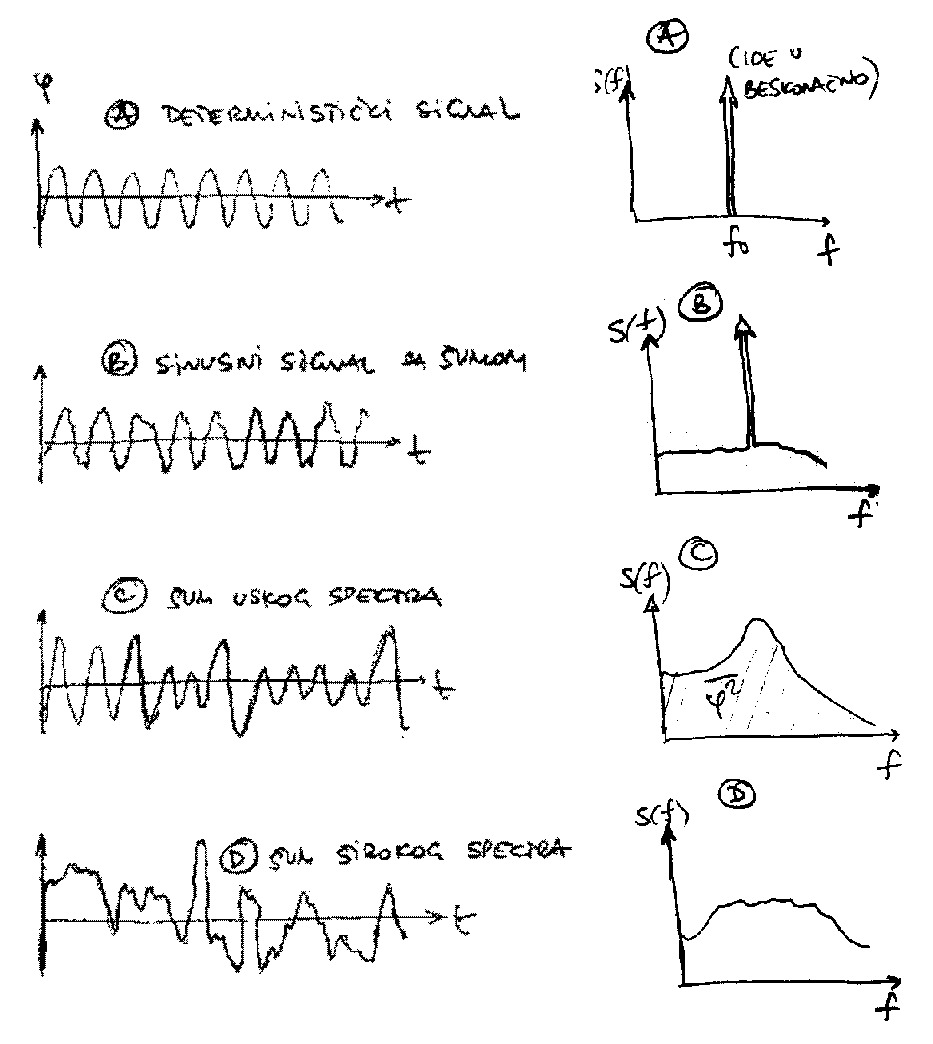
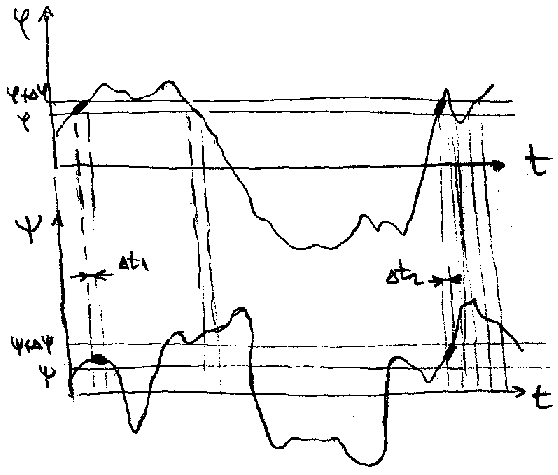
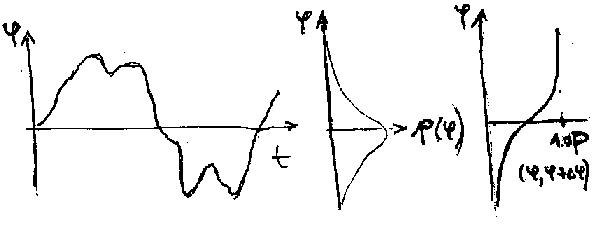
 Oblik krive je zvonast sa tim sto moze biti izduzen u φ ili ψ pravcu ako je to dominantan pravac kretanja (slika 3.39).
Oblik krive je zvonast sa tim sto moze biti izduzen u φ ili ψ pravcu ako je to dominantan pravac kretanja (slika 3.39).
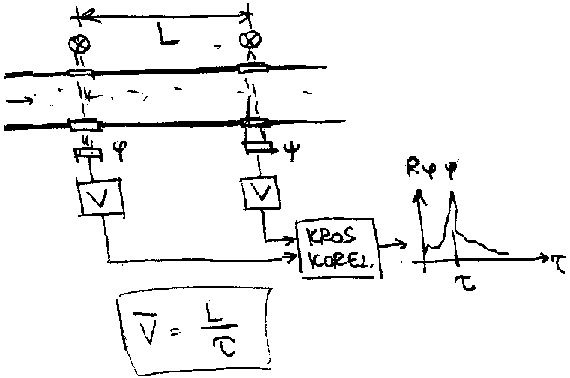 Primer: merenje brzine vode - moglo bi da se napravi u laboratoriji!
Primer: merenje brzine vode - moglo bi da se napravi u laboratoriji!